Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(SA=SB=SC\)nên hình chiếu vuông góc từ \(S\)xuống mặt phẳng đáy là trọng tâm của tam giác \(ABC\).
Gọi \(G\)là trọng tâm tam giác \(ABC\).
\(\widehat{\left(SA,\left(ABC\right)\right)}=\widehat{SAG}\)
\(AG=cos60^o.SA=\frac{a}{2}\), \(SG=sin60^o.SA=\frac{a\sqrt{3}}{2}\)
\(\Rightarrow AB=\frac{a\sqrt{3}}{2}\)
\(S_{ABC}=\frac{\left(\frac{a\sqrt{3}}{2}\right)^2\sqrt{3}}{4}=\frac{3a^2\sqrt{3}}{4}\)
\(V_{S.ABC}=\frac{1}{3}SG.S_{ABC}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.\frac{3a^2\sqrt{3}}{4}=\frac{3a^3}{8}\)


2sin^2x+5cosx+1=0
\(2\cdot\left(1-cos^2x\right)+5cosx+1=0\)
\(-2cos^2x+5cosx+3=0\)
\(\orbr{\begin{cases}cosx=3\left(l\right)\\cosx=-\frac{1}{2}\end{cases}}\)
\(cosx=cos\frac{2pi}{3}\)
\(\orbr{\begin{cases}x=\frac{2pi}{3}+k2pi\\x=\frac{-2pi}{3}+k2pi\end{cases}}\)

cos2x.tan6x=sin10x
ĐK : cos6x khác 0
cos2x.sin6x/cos6x=sin10x
sin6xcos2x=sin10xcos6x
1/2(sin8x+sin4x)=1/2(sin16x+sin4x)
sin8x+sin4x=sin16x+sin4x
sin8x=sin16x
sin16x=sin8x
\(\orbr{\begin{cases}16x=8x+k2pi\\16x=\frac{pi}{2}-8x+k2pi\end{cases}}\)
\(\orbr{\begin{cases}16x-8x=k2pi\\16x+8x=\frac{pi}{2}+k2pi\end{cases}}\)
\(\orbr{\begin{cases}8x=k2pi\\24x=\frac{pi}{2}+k2pi\end{cases}}\)
\(\orbr{\begin{cases}x=\frac{kpi}{4}\\x=\frac{pi}{48}+\frac{kpi}{12}\end{cases}\left(k\in Z\right)}\)
sin^2(4x)+cos^2(6x)=1
\(\frac{1-cos8x}{2}+\frac{1+cos12x}{2}=1\)
\(\frac{1}{2}-\frac{1}{2}cos8x+\frac{1}{2}+\frac{1}{2}cos12x=1\)
\(\frac{1}{2}cos12x-\frac{1}{2}cos8x=0\)
\(cos12x-cos8x=0\)
\(-2sin10xsin2x=0\)
\(\orbr{\begin{cases}sin10x=0\\sin2x=0\end{cases}}\)
\(\orbr{\begin{cases}10x=kpi\\2x=kpi\end{cases}}\)
\(\orbr{\begin{cases}x=\frac{kpi}{10}\\x=\frac{kpi}{2}\end{cases}}\)
\(x=\frac{kpi}{10}\left(k\in Z\right)\)

\(2cosx+cos\frac{x}{2}=4cos^2\frac{x}{2}-2+cos\frac{x}{2}=4t^2+t-2=f\left(t\right)\)(\(t=cos\frac{x}{2},-1\le t\le1\))
\(f'\left(t\right)=8t+1\)
\(f'\left(t\right)=0\Leftrightarrow t=-\frac{1}{8}\)
\(f\left(-1\right)=1,f\left(-\frac{1}{8}\right)=\frac{-33}{16},f\left(1\right)=3\)
do đó \(minf\left(t\right)_{t\in\left[-1,1\right]}=min\left\{f\left(-1\right),f\left(-\frac{1}{8}\right),f\left(1\right)\right\}=-\frac{33}{16}\)
\(maxf\left(t\right)_{t\in\left[-1,1\right]}=max\left\{f\left(-1\right),f\left(-\frac{1}{8}\right),f\left(1\right)\right\}=3\)
Để phương trình ban đầu có nghiệm thì \(m\in\left[-\frac{33}{16},3\right]\).

ta có 5 trường hợp tương ứng với các số có từ 1 đến 5 chứ số :
th1: 1 chữ số : ta có 3 số chẵn
th2:2 chữ số : số cuối cùng có 3 lựa chọn, số thử 2 có 5 lựa chọn nên có \(3\times5\) số chẵn
th3:....
th4:...
th5 số cuối cùng có 3 lựa chọn, 4 chữ số còn lại mỗi số có 5 lựa chọn nên có \(3\times5^4\) số chẵn
vậy cộng lại ta có :\(3+3\times5+3\times5^2+3\times5^3+3\times5^4+3\times5^5=3\times\frac{5^6-1}{4}\)số chẵn được lập



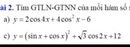
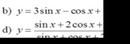

 Giuap mk với giải bt vs ạ
Giuap mk với giải bt vs ạ 