a: Để A là phân số thì \(n+1\ne0\)

=>\(n\ne-1\)

b: Để A là số nguyên thì \(n-3⋮n+1\)

=>\(n+1-4⋮n+1\)

=>\(-4⋮n+1\)

=>\(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)

=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)

Bài 7:

Tỉ số giữa số học sinh giỏi kì 1 với tổng số học sinh là:

\(\dfrac{1}{9+1}=\dfrac{1}{10}\)

Tỉ số giữa số học sinh giỏi kì 2 với tổng số học sinh là:

\(\dfrac{1}{4+1}=\dfrac{1}{5}\)

Số học sinh của lớp là:

\(3:\left(\dfrac{1}{5}-\dfrac{1}{10}\right)=3:\dfrac{1}{10}=30\left(bạn\right)\)

                 Giải:

Tích của bán kính với bán kính của mảnh vườn hình tròn đó là:

        50,24 : 3,14  = 16 (m²)

         Vì 16 = 4 x 4 

Vậy bán kính của mảnh vườn hình tròn đó là: 4 m

          Chu vi của mảnh vườn hình tròn đó là:

        4 x 2 x 3,14 = 25,12 (m)

   Đáp số: 25,12 m

Bình phương bán kính là: 50,24:3,14=16(m²)

mà 16=4x4

nên độ dài bán kính là 4(m)

Chu vi hình tròn là:

4x2x3,14=8x3,14=25,12(m)

a: Xét ΔABC có AB<AC<BC

mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC

nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)

b: Sửa đề: A là trung điểm của BD, DK cắt CA tại N

Xét ΔCDB có

CA,DK là các đường trung tuyến

CA cắt DK tại M

Do đó: M là trọng tâm của ΔCDB

=>\(CM=\dfrac{2}{3}CA=\dfrac{2}{3}\cdot12=8\left(cm\right)\)

c: Sửa đề; Chứng minh B,M,Q thẳng hàng

Gọi I là trung điểm của CA

Đường trung trực của AC cắt CD tại Q 

mà I là trung điểm của AC

nên QI\(\perp\)AC và I là trung điểm của aC

=>QI//DA

Xét ΔCAD có

I là trung điểm của CA

IQ//DA

Do đó: Q là trung điểm của CD

Xét ΔCDB có

M là trọng tâm

Q là trung điểm của CD

Do đó: B,M,Q thẳng hàng

chắc có ấy ạ

a: ΔABC vuông tại B

=>\(AB^2+BC^2=AC^2\)

=>\(AC=\sqrt{12^2+9^2}=15\left(cm\right)\)

b: Xét ΔHBA vuông tại H và ΔHCB vuông tại H có

\(\widehat{HBA}=\widehat{HCB}\left(=90^0-\widehat{HAB}\right)\)

Do đó: ΔHBA~ΔHCB

=>\(\dfrac{HB}{HC}=\dfrac{HA}{HB}\)

=>\(HB^2=HA\cdot HC\)

c: Đề sai rồi bạn

31;42;53;64;75;86;97

31;42;53;64;75;86;97

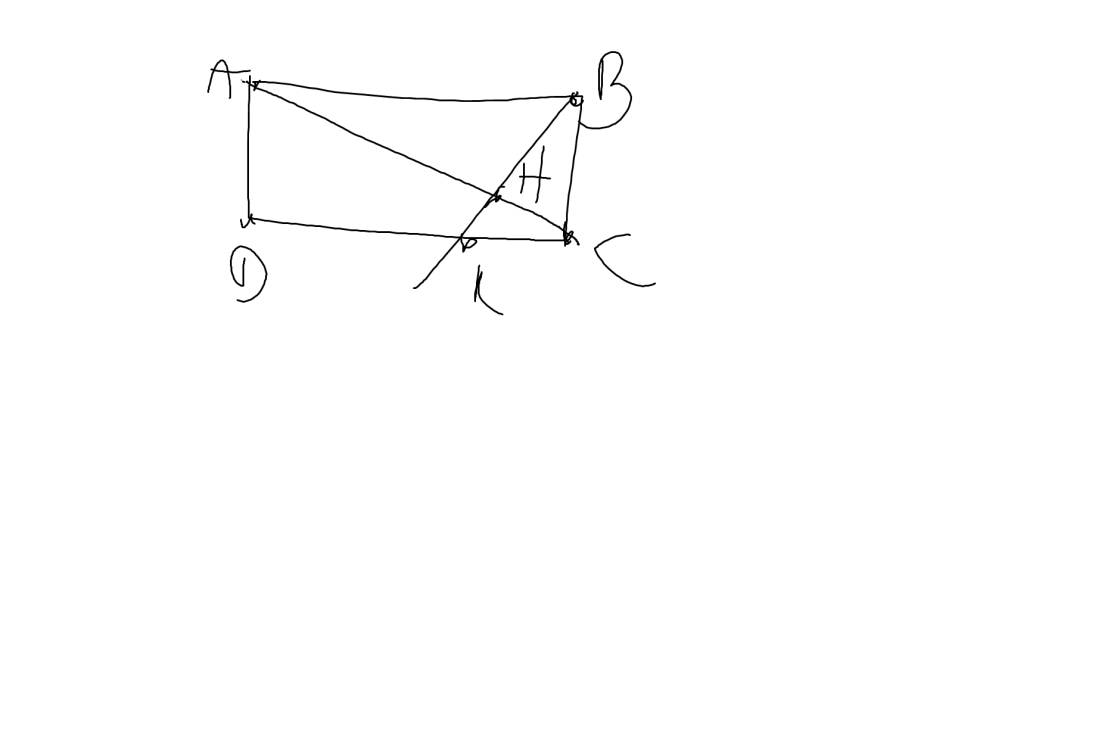
1: Xét ΔABC có 

BN,CM là các đường trung tuyến

BN cắt CM tại D

Do đó: D là trọng tâm của ΔABC

=>\(BD=\dfrac{2}{3}BN;CD=\dfrac{2}{3}CM\)

BD=2/3BN

=>\(S_{ABD}=\dfrac{2}{3}\cdot S_{ABN}\left(1\right)\)

\(CD=\dfrac{2}{3}CM\)

=>\(S_{ADC}=\dfrac{2}{3}\cdot S_{AMC}\left(2\right)\)

Ta có: M là trung điểm của AB

=>\(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}\left(3\right)\)

Ta có: N là trung điểm của AC

=>\(S_{ABN}=\dfrac{1}{2}\cdot S_{ABC}\left(4\right)\)

Từ (1),(2),(3),(4) suy ra \(S_{ABN}=S_{ADC}\)

mà \(S_{MBN}=\dfrac{1}{2}\cdot S_{ANB}\)

và \(S_{MNC}=\dfrac{1}{2}\cdot S_{AMC}\)

nên \(S_{MBN}=S_{MNC}\)

=>\(S_{MBD}+S_{MDN}=S_{NDC}+S_{MDN}\)

=>\(S_{MBD}=S_{NDC}\)

2: \(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot30=15\left(cm^2\right)\)

=>\(S_{MNC}=\dfrac{1}{2}\cdot S_{AMC}=7,5\left(cm^2\right)\)

Vì CD=2/3CM

nên \(S_{CND}=\dfrac{2}{3}\cdot S_{CNM}=5\left(cm^2\right)\)

\(AN=\dfrac{2}{3}AC\)

=>AC=1,5AN

=>\(S_{AMC}=1,5\times S_{AMN}=1,5\times20=30\left(cm^2\right)\)

BM=1/3BC

=>\(CM=\dfrac{2}{3}CB\)

=>CB=1,5CM

=>\(S_{ABC}=1,5\times S_{AMC}=1,5\times30=45\left(cm^2\right)\)

Mik ko bt *^*

1 tuần có 7 ngày 

mà tháng 5 có 31 ngày

và 9 < 31

= > thứ 5 tuần sau vẫn thuộc tháng 5

=  > Thứ 5 tuần sau là ngày : 9 + 7 = 16

Thứ 5 tuần sau là ngày 16 tháng 5

bạn Trần Nguyễn Phương Thảo làm đúng nhưng trả lời hơi thừa