Em cần làm gì với biểu thức này?

Gọi giá của mỗi ly kem ban đầu là x ngàn đồng (x>10)

Giá của mỗi ly kem kể từ ly thứ 10 là: \(x-10\) (ngàn đồng)

Giá tiền của 40 ly kem chưa tính khuyến mãi 20% là:

\(9x+31.\left(x-10\right)=40x-310\) (ngàn đồng)

Giá tiền sau khi giảm 20% trên hóa đơn là:

\(\left(40x-310\right).\left(100\%-20\%\right)=0,8.\left(40x-310\right)\)

Do lớp 9A phải trả 712 ngàn đồng nên ta có pt:

\(0,8\left(40x-310\right)=712\)

 \(\Rightarrow x=30\) (ngàn đồng)

Vậy mỗi ly kem ban đầu có giá 30000 đồng

Ở câu b, đề là \(\widehat{ADF}+\) cái gì \(=90^0\) độ em ha?

a: Thay m=3 vào phương trình, ta được:

\(x^2+4x+3=0\)

=>(x+1)(x+3)=0

=>\(\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)

b: \(\text{Δ}=4^2-4\cdot1\cdot m=-4m+16\)

Để phương trình có hai nghiệm phân biệt thì Δ>0

=>-4m+16>0

=>-4m>-16

=>m<4

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-4\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)

\(2x_1x_2=x_1+x_2+10\)

=>2m=-4+10=6

=>m=3(nhận)

Gọi chiều rộng của mảnh đất là x (m) với x>0

Chiều dài của mảnh đất là: \(x+4\) (m)

Diện tích mảnh đất là: \(x\left(x+4\right)\) (m)

Do diện tích mảnh đất là 285 \(m^2\) nên ta có pt:

\(x\left(x+4\right)=285\)

\(\Leftrightarrow x^2+4x-285=0\Rightarrow\left[{}\begin{matrix}x=15\\x=-19< 0\left(loại\right)\end{matrix}\right.\)

Vậy chiều rộng mảnh đất là 15m, chiều dài là \(15+4=19\)m

Chu vi mảnh đất là: \(\left(15+19\right).2=68\left(m\right)\)

a.

\(\Delta'=\left(-3\right)^2-2.3=3>0\) nên pt đã cho có 2 nghiệm pb

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=\dfrac{3}{2}\end{matrix}\right.\)

b.

\(A=\dfrac{2x_1-x_2}{x_1}-\dfrac{x_1-2x_2}{x_2}=\dfrac{2x_1}{x_1}-\dfrac{x_2}{x_1}-\dfrac{x_1}{x_2}+\dfrac{2x_2}{x_2}\)

\(=4-\left(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}\right)=4-\left(\dfrac{x_1^2+x_2^2}{x_1x_2}\right)=4-\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}\)

\(=4-\dfrac{3^2-2.\dfrac{3}{2}}{\dfrac{3}{2}}=4-4=0\)

a: Xét tứ giác AOBM có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)

nên AOBM là tứ giác nội tiếp

b: Xét ΔAOM vuông tại A có \(sinAMO=\dfrac{AO}{OM}=\dfrac{1}{2}\)

nên \(\widehat{AMO}=30^0\)

Xét (O) có

MA,MB là các tiếp tuyến

DO đó: MA=MB và MO là phân giác của góc AMB

MO là phân giác của góc AMB

=>\(\widehat{AMB}=2\cdot\widehat{AMO}=60^0\)

AOBM nội tiếp

=>\(\widehat{AOB}+\widehat{AMB}=180^0\)

=>\(\widehat{AOB}=120^0\)

Độ dài đường tròn (O) là:

\(C=2\cdot5\cdot3,14=31,4\left(cm\right)\)

Diện tích hình quạt tròn ứng với cung nhỏ AB là:

\(S_{q\left(AB\right)}=\Omega\cdot5^2\cdot\dfrac{120}{360}=5^2\cdot\dfrac{3.14}{3}=\dfrac{157}{6}\left(cm^2\right)\)

c: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: OM là phân giác của góc AOB

=>\(\widehat{AOM}=\widehat{BOM}=\dfrac{120^0}{2}=60^0\)

Xét ΔOAC có OA=OC và \(\widehat{AOC}=60^0\)

nên ΔOAC đều

=>AC=OC=OA=R

Xét ΔOCB có OC=OB và \(\widehat{COB}=60^0\)

nên ΔOCB đều

=>OC=CB=OB=R

Xét tứ giác OACB có

OA=AC=CB=OB

nên OACB là hình thoi

           Giải:

Câu a tự làm

b; Phương trình hoành độ giao điểm của (p) và (d) là:

             \(x^2\) = - 2\(x\) + 3

              \(x^2\) + 2\(x\) - 3 = 0

              a + b + c = 1 + 2  - 3 = 0

      Vậy phương trình có hai nghiệm phân biệt lần lượt là:

              \(x_1\) = 1; \(x_2\) = - 3

\(x_1\) = 1 ⇒ y1 = 1² = 1;  \(x_2\) = - 3 ⇒ y₂ =  (\(x_2\))² = (- 3)² = 9

Vậy (p) cắt (d) tại hai điểm A; B lần lượt có tọa độ là:

A(1; 1); B(-3; 9)

a.

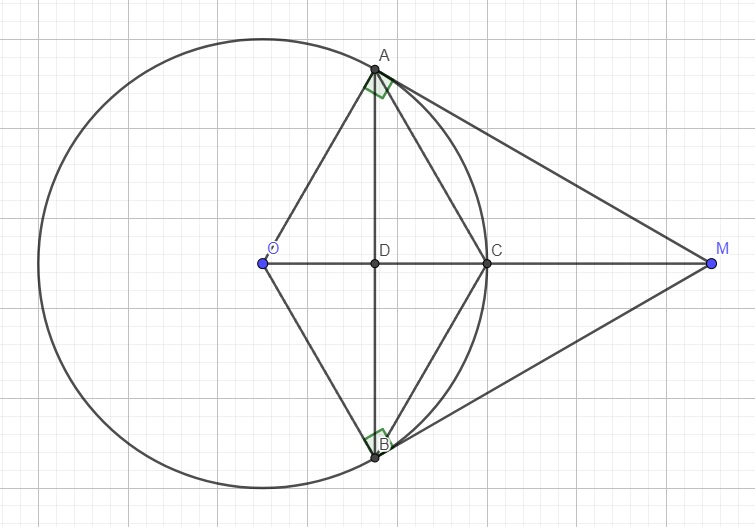
Do MA, MB là các tiếp tuyến \(\Rightarrow\widehat{MAO}=\widehat{MBO}=90^0\)

\(\Rightarrow A,B\) cùng nhìn OM dưới 1 góc vuông nên AOBM nội tiếp

b.

\(C_{\left(O\right)}=2\pi R=10\pi=31,42\left(cm\right)\)

Trong tam giác vuông OAM:

\(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)

\(\Rightarrow\widehat{AOB}=2\widehat{AOM}=120^0\)

\(\Rightarrow S_{OAB}=S_{\left(O\right)}.\dfrac{120}{360}=\dfrac{\pi.R^2}{3}=\dfrac{5^2.\pi}{3}\approx26,18\)

c.

Ta có \(CM=OM-OC=2R-R=R\)

\(\Rightarrow CM=OC\Rightarrow C\) là trung điểm OM

\(\Rightarrow AC\) là trung tuyến ứng với cạnh huyền trong tam giác vuông OAM

\(\Rightarrow AC=\dfrac{1}{2}OM=R=OA\)

Tương tự có BC là trung tuyến ứng với cạnh huyền trong tam giác vuông OBM

\(\Rightarrow BC=OC=R\)

\(\Rightarrow OA=AC=BC=OB\Rightarrow AOBC\) là hình thoi

Gọi D là giao điểm AB và OC \(\Rightarrow AD\perp OC\) (hai đường chéo hình thoi)

Trong tam giác vuông AOD:

\(sin\widehat{AOD}=\dfrac{AD}{OA}\Rightarrow AD=OA.sin\widehat{AOD}=5.sin60^0=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)

\(\Rightarrow AB=2AD=5\sqrt{3}\) (cm)

\(\Rightarrow S_{AOBC}=\dfrac{1}{2}AD.OC=\dfrac{25\sqrt{3}}{2}\approx21,65\left(cm^2\right)\)