12kg 5g=....g
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: SA\(\perp\)(ABCD)
BC\(\subset\left(ABCD\right)\)
Do đó: SA\(\perp\)BC
b: Ta có: DC\(\perp\)AD(ABCD là hình chữ nhật)
DC\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: DC\(\perp\)(SAD)

\(f\left(x\right)⋮g\left(x\right)\)
=>\(2x^2-x+2⋮2x+1\)
=>\(2x^2+x-2x-1+3⋮2x+1\)
=>\(3⋮2x+1\)
=>\(2x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-1;1;-2\right\}\)

\(8,75\times x+1,25\times x=20\)
\(=>\left(8,75+1,25\right)\times x=20\)
\(=>10\times x=20\)
\(=>x=20:10\)
\(=>x=2\)
Vậy...
`#NqHahh`
Cho a,b,c là các số thực dương thỏa mãn a+b+c=6
Tìm GTNN của biểu thức A= a2/ a+b + b2/ c+a + c2/b+c

Lời giải:
Áp dụng BĐT Cauchy Schwarz:
$A=\frac{a^2}{a+b}+\frac{b^2}{c+a}+\frac{c^2}{b+c}\geq \frac{(a+b+c)^2}{a+b+c+a+b+c}=\frac{(a+b+c)^2}{2(a+b+c)}=\frac{a+b+c}{2}\geq \frac{6}{2}=3$
Vậy $A_{\min}=3$. Giá trị này đạt tại $a=b=c=2$

Em viết đề bài bằng công thức toán học biểu tượng \(\Sigma\) bên góc trái màn hình.


1: \(\left(x-\dfrac{1}{2}\right)^2>=0\forall x\)
=>\(A=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
2: \(\left|3x-1\right|>=0\forall x\)
=>\(\left|3x-1\right|-5>=-5\forall x\)
Dấu '=' xảy ra khi 3x-1=0
=>3x=1
=>\(x=\dfrac{1}{3}\)
3: \(\left(2-x\right)^2>=0\forall x\)
=>\(-\left(2-x\right)^2< =0\forall x\)
=>\(C=-\left(2-x\right)^2+5< =5\forall x\)
Dấu '=' xảy ra khi 2-x=0
=>x=2
4: \(\left(x^2-4\right)^2>=0\forall x\)
\(\left|y-x\right|>=0\forall x,y\)
Do đó: \(\left(x^2-4\right)^2+\left|y-x\right|>=0\forall x,y\)
=>\(D=\left(x^2-4\right)^2+\left|y-x\right|+3>=3\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x^2-4=0\\y-x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{2;-2\right\}\\y=x\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y=x=2\\y=x=-2\end{matrix}\right.\)
5: \(\left(x-1\right)^2>=0\forall x\)
\(\left(x^2-1\right)^4>=0\forall x\)
Do đó: \(E=\left(x-1\right)^2+\left(x^2-1\right)^4>=0\forall x\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-1=0\\x^2-1=0\end{matrix}\right.\)
=>x=1
6: \(\left(x+3\right)^2+3>=3\forall x\)
=>\(F=\dfrac{2}{\left(x+3\right)^2+3}< =\dfrac{2}{3}\forall x\)
Dấu '=' xảy ra khi x+3=0
=>x=-3
7: \(\left(x^2+1\right)^2>=1^2=1\forall x\)
=>\(\left(x^2+1\right)^2+2022>=2023\forall x\)
=>\(G=\dfrac{2023}{\left(x^2+1\right)^2+2022}< =\dfrac{2023}{2023}=1\forall x\)
Dấu '=' xảy ra khi x=0

Còn phụ thuộc vào nhiều yếu tố phụ kèm theo nữa em nhé.
+ Hạnh kiểm tốt
+ Không có môn nào dưới 6,5
....

\(3+\dfrac{6}{11}=\dfrac{33}{11}+\dfrac{6}{11}=\dfrac{39}{11}\)
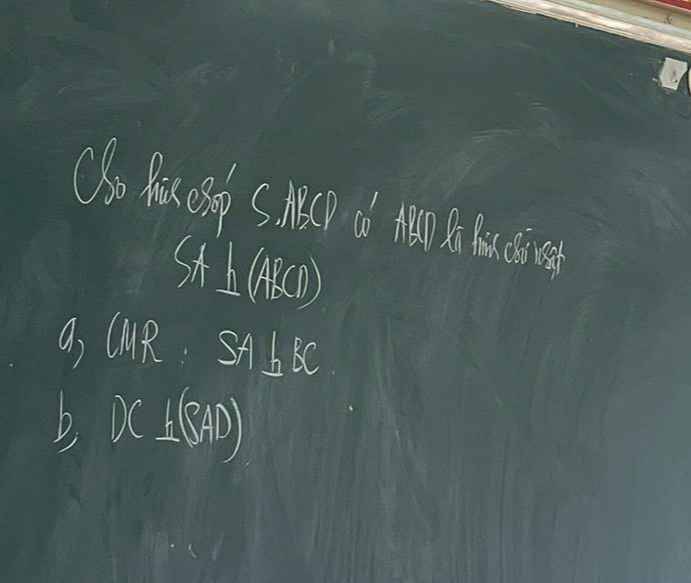
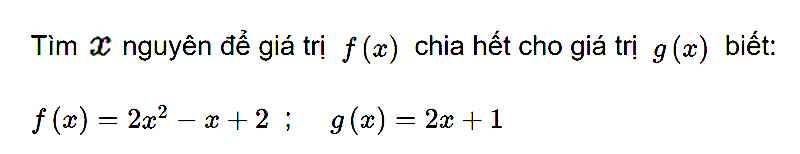
12005
12kg5g=12005g