phân tích 5x^2-20x+20 thành nhân tử
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài làm
~ Đăng lên rồi thì nhắn lại tôi biết chứ trời ạ, còn tưởng chưa đăng cơ~
Bài 3
a) x2 + xy + 5x + 5y b) x2 - y2 + 3x - 3y
= x(x + y) + 5(x + y) = (x2 - y2) + 3(x - y)
= (x + 5)(x + y) = (x + y)(x - y) + 3(x - y)
= (x + y + 3)(x - y)
c) x2 - 8x + 16 - y2 d) 4x2 - y2 + 10y - 25
= (x2 - 8x + 16) - y2 = 4x2 - (y2 - 10y + 25)
= (x - 4)2 - y2 = 4x2 - (y - 5)2
= (x - 4 - y)(x - 4 + y) = (4x - y + 5)(4x + y - 5)
Bài 4
a) 2x(x - 7) + 5x - 35 = 0
<=> 2x(x - 7) + 5(x - y) = =
<=> (2x + 5)(x - 7) = 0
<=> \(\orbr{\begin{cases}2x+5=0\\x-7=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{2}\\x=7\end{cases}}}\)
Vậy x = -5/2 hoặc x = 7
b) x(x - 3) - 7x + 21 = 0
<=> x(x - 3) - 7(x - 3) = 0
<=> (x - 7)(x - 3) = 0
<=> \(\orbr{\begin{cases}x-7=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}}\)
Vậy x = 7 hoặc x = 3
c) x3 - 2x2 + x - 2 = 0
<=> x2(x - 2) + (x - 2) = 0
<=> (x2 + 1)(x - 2) = 0
<=> \(\orbr{\begin{cases}x^2+1=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x^2=-1\left(v\text{ô}-l\text{í}\right)\\x=2\end{cases}}}\)
Vậy x = 2
d) x3 - 5x2 - x + 5 = 0
<=> x2(x - 5) - (x - 5) = 0
<=> (x2 - 1)(x - 5) = 0
<=> x2 - 1 = 0 hoặc x - 5 = 0
<=> x2 = 1 hoặc x = 5
<=> x = 1 hoặc x = -1 hoặc x = 5
Vậy x = 1 hoặc x = -1 hoặc x = 5

\(M=2a^3+2b^3-3\left(a^2+b^2\right)=2\left(a^3+b^3\right)-3\left(a^2+b^2\right)\)
\(=2\left[\left(a+b\right)^3-3ab\left(a+b\right)\right]-3\left[\left(a+b\right)^2-2ab\right]\)
\(=2\left(a+b\right)^3-6ab-3\left(a+b\right)^2+6ab\)
\(=2\left(a+b\right)^3-3\left(a+b\right)^2=2-3=-1\)

\(\hept{\begin{cases}3x+2y=16\\2x-5y=-2\end{cases}}\Leftrightarrow\hept{\begin{cases}6x+4y=32\\6x-15y=-6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}19y=38\\x=\frac{-2+5y}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}y=2\\x=\frac{-2+10}{2}=4\end{cases}}\)
Vậy hft có một nghiệm (x;y) = (4;2)
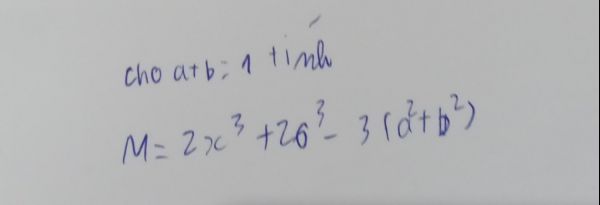
 Help mình câu này nha
Help mình câu này nha