a, vì  1.16 = 2.8

Vậy ta có các tỉ lệ thức: \(\dfrac{1}{2}\) = \(\dfrac{8}{16}\); \(\dfrac{1}{8}\) = \(\dfrac{2}{16}\); \(\dfrac{2}{1}\) = \(\dfrac{16}{8}\); \(\dfrac{16}{2}\) = \(\dfrac{8}{1}\)

b, \(\dfrac{3}{2}\) : \(\dfrac{2}{3}\) = \(\dfrac{1}{4}\) : \(\dfrac{1}{9}\) ⇒ \(\dfrac{3}{2}\).\(\dfrac{1}{9}\) = \(\dfrac{1}{4}\).\(\dfrac{2}{3}\)

     \(\dfrac{3}{2}\) : \(\dfrac{1}{4}\) = \(\dfrac{2}{3}\)  : \(\dfrac{1}{9}\)

      \(\dfrac{1}{9}\) :  \(\dfrac{1}{4}\) = \(\dfrac{2}{3}\) : \(\dfrac{3}{2}\)

      \(\dfrac{1}{9}\) : \(\dfrac{2}{3}\) = \(\dfrac{1}{4}\) : \(\dfrac{3}{2}\) 

Lời giải:
Với $x\geq -1$ thì: $A=x+3|x+1|=x+3(x+1)=4x+3$ không có GTLN, vì bạn cứ cho giá trị x càng lớn thì $A$ càng lớn. Giá trị x lớn không có điểm dừng thì A cũng lớn không có điểm dừng.

Bạn xem lại đề xem đã viết đúng chưa vậy?

a,     (\(\dfrac{9}{10}\) - \(\dfrac{15}{16}\)) \(\times\) ( \(\dfrac{5}{12}\) - \(\dfrac{11}{15}\) - \(\dfrac{7}{20}\))

=  (\(\dfrac{72}{80}\) - \(\dfrac{75}{80}\))  \(\times\) (\(\)\(\dfrac{25}{60}\) - \(\dfrac{44}{60}\)  - \(\dfrac{21}{60}\))

= - \(\dfrac{3}{80}\)  \(\times\) (- \(\dfrac{2}{3}\))

= \(\dfrac{1}{40}\) 

b, (-1)³ + (- \(\dfrac{2}{3}\))² : 2\(\dfrac{2}{3}\) + \(\dfrac{5}{6}\)

=  -1³ +   \(\dfrac{4}{9}\) : \(\dfrac{8}{3}\) + \(\dfrac{5}{6}\)

= -1 + \(\dfrac{4}{9}\) \(\times\) \(\dfrac{3}{8}\) + \(\dfrac{5}{6}\)

= -1 + \(\dfrac{1}{6}\) + \(\dfrac{5}{6}\)
= -1 + 1

= 0

Để x + 2y và 2x - y là số hữu tỷ, ta có thể thiết lập hệ phương trình sau:

x + 2y = a/b (1)

2x - y = c/d (2)

Trong đó a, b, c, d là các số nguyên và b, d khác 0.

Từ phương trình (1), ta có x = a/b - 2y. Thay vào phương trình (2), ta có:

2(a/b - 2y) - y = c/d

2a/b - 4y - y = c/d

2a/b - 5y = c/d

Để 2a/b - 5y là số hữu tỷ, ta cần 5y cũng là số hữu tỷ. Vì vậy, y phải là số hữu tỷ.

Tiếp theo, để x = a/b - 2y là số hữu tỷ, ta cần a/b - 2y cũng là số hữu tỷ. Vì y là số hữu tỷ, nên a/b - 2y cũng là số hữu tỷ.

Vậy, nếu x + 2y và 2x - y là số hữu tỷ, thì x và y đều là số hữu tỉ.

\(\left(\dfrac{5}{6}x+3\right)^2=\dfrac{4}{9}\)

\(\Rightarrow\left(\dfrac{5}{6}x+3\right)^2=\left(\pm\dfrac{2}{3}\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}\dfrac{5}{6}x+3=\dfrac{2}{3}\\\dfrac{5}{6}x+3=-\dfrac{2}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\dfrac{5}{6}x=-\dfrac{7}{3}\\\dfrac{5}{6}x=-\dfrac{11}{3}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{14}{5}\\x=-\dfrac{22}{5}\end{matrix}\right.\)

\(\dfrac{11}{12}x+0,25=\dfrac{5}{6}\\ \dfrac{11}{12}x=\dfrac{5}{6}-\dfrac{1}{4}=\dfrac{7}{12}\\ x=\dfrac{7}{12}:\dfrac{11}{12}=\dfrac{7}{11}\)

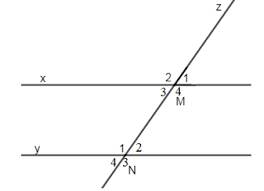
không nhé như hình (hình 2) này trong cùng phía là N2 và M4.

Hình 1 có 2 góc zOy và góc xOy là 2 góc kề bù và có tổng 180 độ

KO

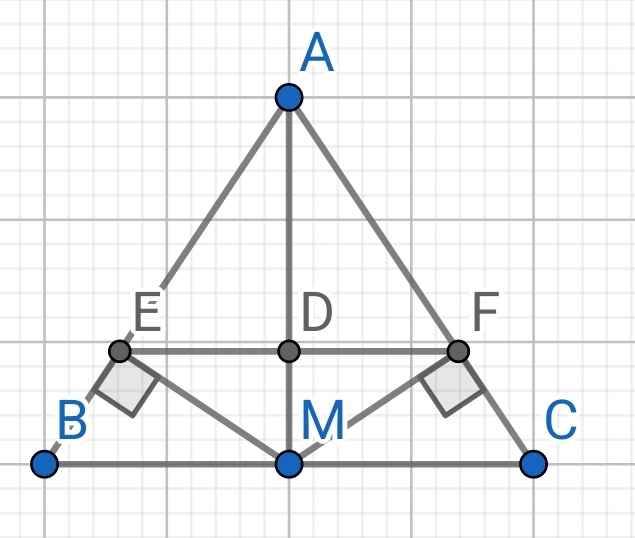 a) Do M là trung điểm của BC (gt)

⇒ BM = CM

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆AMB và ∆AMC có:

AM là cạnh chung

AB = AC (cmt)

BM = CM (cmt)

⇒ ∆AMB = ∆AMC (c-c-c)

b) Sửa đề:

Chứng minh AM EF

Giải:

Gọi D là giao điểm của AM và EF

Do ∆AMB = ∆AMC (cmt)

⇒ ∠MAB = ∠MAC (hai góc tương ứng)

⇒ ∠MAE = ∠MAF

Xét hai tam giác vuông: ∆MAE và ∆MAF có:

AM là cạnh chung

∠MAE = ∠MAF (cmt)

⇒ ∆MAE = ∆MAF (cạnh huyền - góc nhọn)

⇒ AE = AF (hai cạnh tương ứng)

Do ∠MAE = ∠MAF (cmt)

⇒ ∠DAE = ∠DAF 

Xét ∆ADE và ∆ADF có:

AD là cạnh chung

∠DAE = ∠DAF (cmt)

AE = AF (cmt)

⇒ ∆ADE = ∆ADF (c-g-c)

⇒ ∠ADE = ∠ADF (hai góc tương ứng)

Mà ∠ADE + ∠ADF = 180⁰ (kề bù)

⇒ ∠ADE = ∠ADF = 180⁰ : 2 = 90⁰

⇒ AD ⊥ EF

.