cho tam giác ABC , biết góc A có số đo bằng 120 độ . Các đường trung trực của AB và AC cắt nhau tại D và lần lượt tại E và F .
a) chứng minh tam giác ABE là tam giác cân .
b) chứng minh tam giác ADF bằng tam giác CDF .
c) tính số đo góc EAD .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2,3x30+6,9x45+20,7x15
=2,3x30+2,3x135+2,3x135
=2,3x(30+135+135)
=2,3x300=690

Có \(AC=AD\sqrt{2}=a\sqrt{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\) \(\Rightarrow\Delta SAC\) vuông tại A.
\(\Rightarrow SA=\sqrt{SC^2-AC^2}=\sqrt{\left(a\sqrt{3}\right)^2-\left(a\sqrt{2}\right)^2}=a\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.S_{ABCD}.SA=\dfrac{1}{3}.AD^2.SA=\dfrac{1}{3}.a^2.a=\dfrac{a^3}{3}\)

Giải:
Cứ 1 điểm sẽ tạo với n - 1 điểm còn lại n - 1 đường thẳng
với n điểm sẽ tạo được (n - 1)n đường thẳng
Theo cách tính trên mỗi đường thẳng sẽ được tính hai lần nên thực tế số đường thẳng được tạo là:
(n - 1).n : 2 (đường thẳng)
Theo bài ra ta có: (n - 1)n : 2 = 105
(n - 1)n = 105.2
(n - 1).n = 210
(n - 1).n = 14.15
n = 15
Vậy n = 15

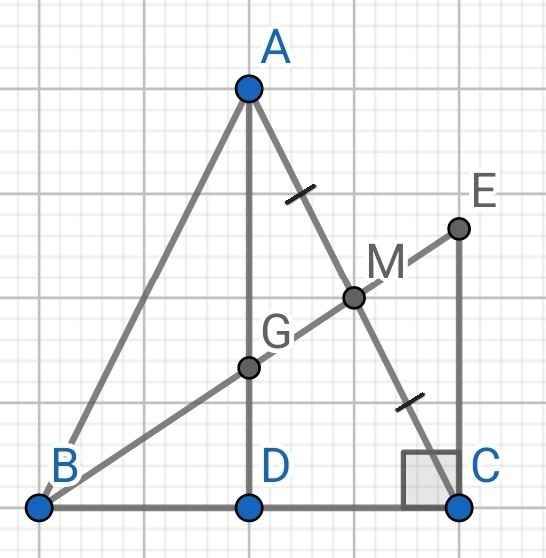
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Do AD là đường phân giác của ∆ABC (gt)
⇒ ∠BAD = ∠CAD
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
b) ∆ABC cân tại A (gt)
AD là đường phân giác (gt)
⇒ AD cũng là đường cao của ∆ABC
⇒ AD ⊥ BC
c) Do CE ⊥ BC (gt)
AD ⊥ BC (cmt)
⇒ AD // CE
⇒ ∠GAM = ∠ECM (so le trong)
Do BM là đường trung tuyến của ∆ABC (gt)
⇒ M là trung điểm của AC
⇒ AM = CM
Xét ∆AGM và ∆CEM có:
∠GAM = ∠ECM (cmt)
AM = CM (cmt)
∠AMG = ∠CME (đối đỉnh)
⇒ ∆AGM = ∆CEM (g-c-g)

a) \(\Delta'=\left(m-2\right)^2-\left(-3m+10\right)=m^2-m-6\)
Để phương trình có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2\\m\ge3\end{matrix}\right.\) (1)
Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=4-2m\\x_1x_2=-3m+10\end{matrix}\right.\)
Để phương trình có 2 nghiệm x1, x2 đều nhỏ hơn 2 \(\left(x_1\le x_2< 2\right)\) thì:
\(\left\{{}\begin{matrix}\left(x_1-2\right)+\left(x_2-2\right)< 0\\\left(x_1-2\right)\left(x_2-2\right)>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2< 4\\x_1x_2-2\left(x_1+x_2\right)+4>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4-2m< 4\\-3m+10-2\left(4-2m\right)+4>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2m< 0\\m+6>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>-6\end{matrix}\right.\Leftrightarrow m>0\)
Kết hợp với điều kiện (1), ta được: \(m\ge3\)
\(Toru\)

Đây là toán nâng cao chuyên đề hình khối, cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
a; Thể tích của một hình lập phương nhỏ là:
10 x 10 x 10 = 1000 (cm3)
Thể tích của hình lập phương H là;
1000 x 8 = 8000 (cm3)
Vì 20 x 20 x 20 = 8000
Vậy cạnh của hình lập phương H là: 20 cm
b; Diện tích một mặt của hình lập phương H là:
20x 20 = 400 (cm2)
Diện tích toàn phần của hình lập phương H là:
400 x 6 = 2400(cm2)
Đáp số:a; 8000 cm3
b; 2400 cm2

Đây là dạng toán nâng cao chuyên đề giả thiết tạm, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Giả sử tất cả đều là tờ tiền 50 000 đồng thì tổng số tiền là
50 000 x 13 = 650 000 (đồng)
So với đề bài thì thừa ra:
650 000 - 300 = 350 000 (đồng)
Vì số tờ tiền 10 000 đồng bằng số tờ tiền 20 000 đồng nên ta thay 2 tờ 50 000 đồng bằng 1 tờ tiền 10 000 đồng và 1 tờ tiền 20 000 thì cứ sau mỗi lần thay như vậy, số tiền giảm là:
50 000 x 2 - (10 000 + 10 000 ) = 70 000 (đồng)
Số tờ tiền 10 000 bằng số tờ tiền 20 000 và bằng:
350 000 : 70 000 = 5 (tờ)
Số tờ tiền 50 000 đồng là:
13 - 5 - 5 = 3 (tờ)
Đáp số: số tờ tiền 10 000 đồng là 5 tờ
số tờ tiền 20 000 đồng là 5 tờ
số tờ tiền 50 000 đồng là 3 tờ.

Số kiểu chậu khác nhau là \(\dfrac{A^5_{20}}{5}=372096\) (chọn 5 số có kể thứ tự từ 20 số và chia cho số hoán vị vòng quanh của mỗi hoán vị phân biệt)
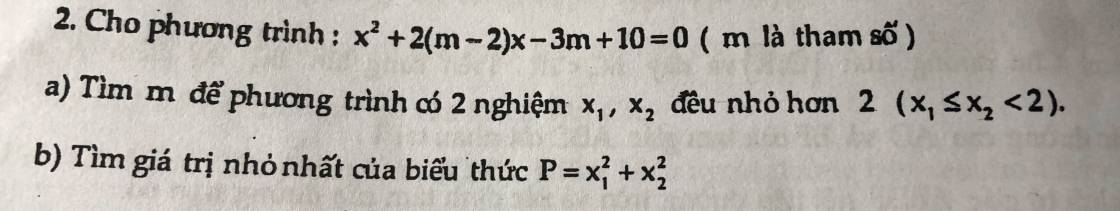
A B C D E F M N
a/ Xét tg ABE có
\(DM\perp AB\Rightarrow EM\perp AB\)
=> tg ABE cân tại E (Tam giác có đường cao đồng thời là đường trunbg trực thì tg đó là tg cân)
b/
Xét tg ACF, chứng minh tương tự câu a => tg ACF cân tại F
=> AF = CF (1)
Xét tg ACD, chứng minh tương tự => tg ACD cân tại D
=> AD = CD (2)
Xét tg ADF và tg CDF có
DF chung (3)
Từ (1) (2) (3) => tg ADF = tg CDF (c.c.c)
c/
Xét tg ABD, chứng minh tương tự câu a => tg ABD cân tại D
\(\Rightarrow\widehat{ABD}=\widehat{BAD}\)
Ta có tg ACD cân (cmt) \(\Rightarrow\widehat{CAD}=\widehat{ACD}\)
\(\Rightarrow\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=120^o=\widehat{ABD}+\widehat{ACD}\)
Xét tứ giác ABDC có
\(\widehat{BDC}=360^o-\widehat{BAC}-\left(\widehat{ABD}+\widehat{ACD}\right)\) (Tổng các góc trong của 1 tứ giác bằng \(360^o\))
\(\Rightarrow\widehat{BDC}=360^o-120^o-120^o=120^o\)
Ta có
tg ABD cân tại D (cmt) => AD = BD
tg ACD cân tại D (cmt) => AD = CD
=> BD = CD => tg BCD cân tại D \(\Rightarrow\widehat{CBD}=\widehat{BCD}\) (4)
Xét tg cân BCD có
\(\widehat{CBD}+\widehat{BCD}=180^o-\widehat{BDC}=180^o-120^o=60^o\) (5)
Từ (4) và (5) \(\Rightarrow\widehat{CBD}=\widehat{BCD}=\dfrac{60^o}{2}=30^o\)
Chứng minh tương tự câu b => tg DE = tg BDE (c.c.c)
\(\Rightarrow\widehat{EAD}=\widehat{CBD}=30^o\)