a, C/m CP // AB
Xét ΔANM và ΔCNP. Ta có:
NM = NP (gt)
∠N₁ = ∠N₂ (đối đỉnh)
NA = NC (gt)
⇒ ΔANM = ΔCNP (c.g.c)
Nên: ∠A = ∠C₁ (hai góc tương ứng)
Mà ∠A và ∠C₁ ở vị trí so le trong
⇒ CP // AB
b, C/m MB = CP
Ta có: MA = CP (vì ΔANM = ΔCNP)
Mà MA = MB (gt)
⇒ MB = CP
c, C/m BC = 2MN
Nối BP. Xét ΔMBP và ΔCPB. Ta có:
BM = CP (gt)
∠B₁ = ∠P₁ (so le trong)
BP cạnh chung
⇒ ΔMBP = ΔCPB (c.g.c)
Nên: MP = BC (hai cạnh tương ứng)
Mà: MP = 2MN (vì N là trung điểm của MP)
⇒ BC = 2MN
 

\(\dfrac{1}{2}+1^{2022}\)

\(=\dfrac{1}{2}+1\)

\(=\dfrac{1}{2}+\dfrac{2}{2}\)

\(=\dfrac{1+2}{2}\)

\(=\dfrac{3}{2}\)

Ta có: 1^2022 = 1

Vì 1/2 < 1 nên 1/2 < 1^2022.

Chưa chắc đâu nha =)

Bạn cần viết một đoạn văn hay một đoan văn ạ?

- Tên của bài thơ "Tiếng vọng hòa bình"

- Vần có trong bài thơ: "ôi" ( hồi - rồi ), "ât" ( vật - mất )

- Hình ảnh có trong bài thơ: "cảnh vật", "bóng người", "chiến trường", "áo", "hòa bình", "Tổ quốc".

\(3^{x+1}=9^x\\ \Leftrightarrow3^{x+1}=3^{2x}\\ \Leftrightarrow x+1=2x\\ \Leftrightarrow x=1\)

\(VP=9^x=\left(3^2\right)^x=3^{2x}\\ Vì:3^{x+1}=9^x=3^{2x}\\ Nên:x+1=2x\\ \Rightarrow2x-x=1\\ Vậy:x=1\)

\(a=4^5.9^4-2.\dfrac{6^9}{2^{10}}.3^8+6^8.20\)

Đề là như vầy đúng ko bn?

Bài 2:

a) \(2\left|x-1\right|=\left|-\dfrac{1}{3}\right|+\dfrac{2}{3}\)

\(\Rightarrow2\left|x-1\right|=\dfrac{1}{3}+\dfrac{2}{3}\)

\(\Rightarrow2\left|x-1\right|=1\)

\(\Rightarrow\left|x-1\right|=\dfrac{1}{2}\)

TH1: \(x-1=\dfrac{1}{2}\left(x>1\right)\)

\(\Rightarrow x=\dfrac{1}{2}+1\)

\(\Rightarrow x=\dfrac{3}{2}\) (tm) 

TH2: \(x-1=-\dfrac{1}{2}\left(x< 1\right)\)

\(\Rightarrow x=-\dfrac{1}{2}+1\)

\(\Rightarrow x=\dfrac{1}{2}\) (tm)

b) \(5^x+5^{x+2}=650\)

\(\Rightarrow5^x\cdot\left(1+5^2\right)=650\)

\(\Rightarrow5^x\cdot26=650\)

\(\Rightarrow5^x=\dfrac{650}{26}\)

\(\Rightarrow5^x=25\)

\(\Rightarrow5^x=5^2\)

\(\Rightarrow x=2\)

c) \(\left(2x+\dfrac{1}{2}\right)^2=\dfrac{4}{9}\)

\(\Rightarrow\left(2x+\dfrac{1}{2}\right)^2=\left(\dfrac{2}{3}\right)^2\)

TH1: \(2x+\dfrac{1}{2}=\dfrac{2}{3}\)

\(\Rightarrow2x=\dfrac{2}{3}-\dfrac{1}{2}\)

\(\Rightarrow2x=\dfrac{1}{6}\)

\(\Rightarrow x=\dfrac{1}{12}\)

TH2: \(2x+\dfrac{1}{2}=-\dfrac{2}{3}\)

\(\Rightarrow2x=-\dfrac{2}{3}-\dfrac{1}{2}\)

\(\Rightarrow2x=-\dfrac{7}{6}\)

\(\Rightarrow x=-\dfrac{7}{12}\)

d) \(5-3\sqrt{x}=2\)(\(x\ge0\))

\(\Rightarrow3\sqrt{x}=5-2\)

\(\Rightarrow3\sqrt{x}=3\)

\(\Rightarrow\sqrt{x}=\dfrac{3}{3}\)

\(\Rightarrow\sqrt{x}=1\)

\(\Rightarrow x=1\left(tm\right)\)

Bài 1.

\(M=\sqrt{2\dfrac{14}{25}}+\dfrac{0,6-\dfrac{3}{7}-\dfrac{3}{13}}{1-\dfrac{5}{7}-\dfrac{5}{13}}+\left|-\dfrac{4}{5}\right|+2023^0\)

\(M=\sqrt{\dfrac{64}{25}}+\dfrac{3\cdot\left(\dfrac{1}{5}-\dfrac{1}{7}-\dfrac{1}{13}\right)}{5\cdot\left(\dfrac{1}{5}-\dfrac{1}{7}-\dfrac{1}{13}\right)}+\dfrac{4}{5}+1\)

\(M=\dfrac{8}{5}+\dfrac{3}{5}+\dfrac{4}{5}+1=3+1=4\)

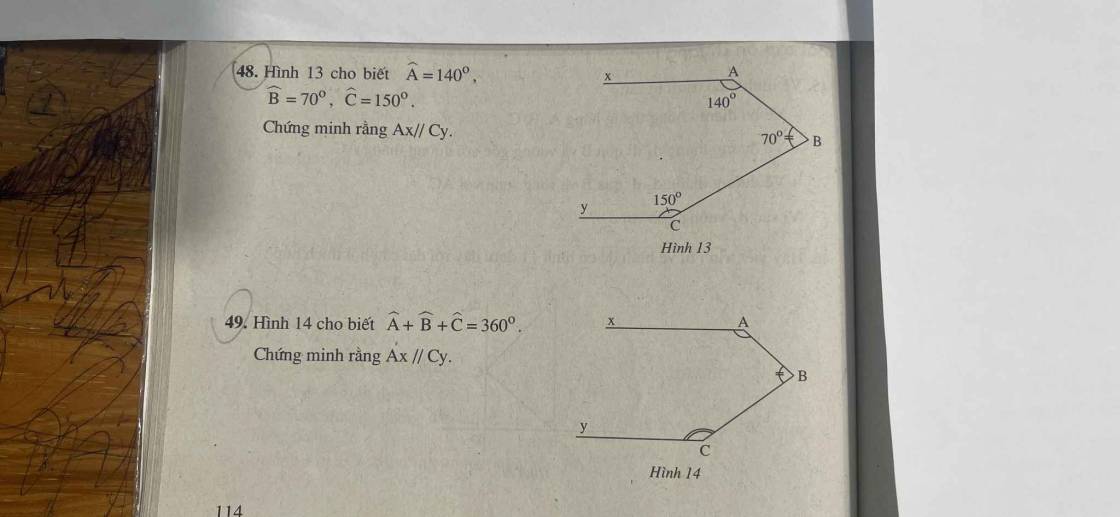
48.

Gọi O là giao của Ax với BC. Xét tg ABO có

\(\widehat{OAB}=\widehat{xAO}-\widehat{xAB}=180^o-140^o=40^o\)

\(\widehat{OBA}=\widehat{CBO}-\widehat{ABC}=180^o-70^o=110^o\)

\(\Rightarrow\widehat{AOB}=180^o-\left(\widehat{OAB}+\widehat{OBA}\right)=180^o-\left(40^o+110^o\right)=30^o\)

\(\Rightarrow\widehat{yCB}+\widehat{AOB}=150^o+30^o=180^o\) hai góc này nằm ở vị trí 2 góc trong cùng phía và bù nhau => Ax//Cy

49.

Nối A với C. Xét tg ABC có

\(\widehat{BAC}+\widehat{BCA}+\widehat{B}=180^o\)

Ta có

\(\widehat{A}+\widehat{B}+\widehat{C}=360^o\)

\(\Rightarrow\widehat{xAC}+\widehat{BAC}+\widehat{B}+\widehat{yCA}+\widehat{BCA}=360^o\)

\(\Rightarrow\left(\widehat{xAC}+\widehat{yCA}\right)+\left(\widehat{BAC}+\widehat{BCA}+\widehat{B}\right)=360^o\)

\(\Rightarrow\widehat{xAC}+\widehat{yCA}=360^o-\left(\widehat{BAC}+\widehat{BCA}+\widehat{B}\right)=\)

\(=360^o-180^o=180^o\)

Hai góc \(\widehat{xAC}\) và \(\widehat{yCA}\) ở vị trí 2 góc trong cùng phía và bù nhau

=> Ax//Cy