Trên đường thẳng AA' lấy điểm O nằm giữa A và A'. Trên một nữa mặt phẳng bờ AA', vẽ tia OB sao cho \(\widehat{AOB}\) = 45* (45 độ). Trên nửa mặt phẳng còn lại vẽ tia OC sao cho \(\widehat{AOC}\) = 90* (90 độ).
a) Gọi OB' là tia phân giác của \(\widehat{A'OC}\). Chứng tỏ rằng \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là hai góc đối đỉnh.
b) Trên nửa mặt phẳng bờ AA' có chứa tia OB, vẽ tia OD sao cho \(\widehat{DOB}\) = 90* (90 độ). Tính \(\widehat{A'OD}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(B_1=A_1=70^o\)
\(\Rightarrow a//b\) (\(A_1\&B_1\)ở vị trí so le trong)
b) \(A_3=A_1=70^o\) (đối đỉnh)
\(A_4=180-A_1=180-70=110^o\) (góc kề bù)
Tương tự B3; B4...

a, |\(x\)| = \(\dfrac{1}{5}\)
\(\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\)

`@` `\text {Ans}`
`\downarrow`
`(5x+2)^3 = -125?`
`=> (5x+2)^3 = (-5)^3`
`=> 5x+2=-5`
`=> 5x = -5-2`
`=> 5x = -7`
`=> x = -7/5`
Vậy, `x = -7/5`
Hoặc nếu đề ntnay
`(5x+2)^4 = -625`
`=> (5x+2)^4 = -(5)^4`
`=> 5x+2= -5`
`=> 5x = -7`
`=> x = -7/5`

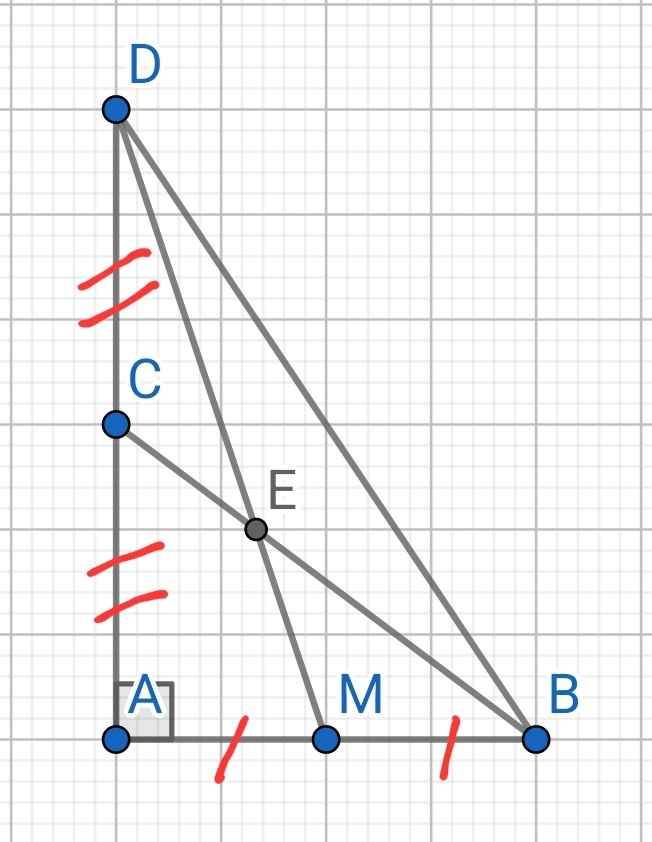
Do CA = CD nên C là trung điểm của AD
Xét ∆ABD có:
C là trung điểm của AD
⇒ BC là đường trung tuyến ứng với cạnh AD (1)
Lại có M là trung điểm AB (gt)
⇒ DM là đường trung tuyến ứng với cạnh AB (2)
Từ (1) và (2) ⇒ E là trọng tâm của ∆ABD
⇒ BE = 2/3 BC = 2/3 . 10 = 20/3 (cm)

1.
\(A=\frac{3}{4}.\frac{4}{5}.\frac{5}{6}(x^{n-1}.x^{2n+1}.x)(y^{2n+1}.y^{n+1})\)
\(=\frac{1}{2}x^{3n+1}y^{3n+2}\)
Hệ số: $\frac{1}{2}$
Bậc của ơơn thức: $3n+1+3n+2=6n+3$
Các bài còn lại bạn làm tương tự.

1) \(\dfrac{4}{5}y^2x^5-x^3.x^2y^2=x^5y^2.\left(\dfrac{4}{5}-1\right)=-\dfrac{1}{5}x^5y^2\)
2) \(-xy^3-\dfrac{2}{7}y^2.xy=-xy^3.\left(1+\dfrac{2}{7}\right)=-\dfrac{9}{7}xy^3\)
3) \(xy^2z\left(\dfrac{5}{6}-\dfrac{1}{4}\right)=\dfrac{7}{12}xy^2z\)
4) \(2x^4\)
5) \(x^5y.\left(\dfrac{1}{2}-\dfrac{3}{4}+1\right)=\dfrac{3}{2}x^5y\)
6) \(x^2\left(11y^5+x^4\right)\)
Xét các số thực a,b,c thỏa mãn 3|a-b|=5|b-c|=7|c-a|. Chứng minh rằng a=b=c.
Ai biết giúp mình với ạ.

TH1: Nếu \(a\ge b\ge c\) thì đk đã cho tương đương với \(3\left(a-b\right)=5\left(b-c\right)=7\left(a-c\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}3a-3b=5b-5c\\5b-5c=7a-7c\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a+5c=8b\\7a-2c=5b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6a+10c=16b\\35a-10c=25b\end{matrix}\right.\) \(\Rightarrow41a=41b\Leftrightarrow a=b\). Điều này có nghĩa là \(a-b=0\), từ đó suy ra \(5\left(b-c\right)=0\Leftrightarrow b=c\). Vậy \(a=b=c\).
TH2: Nếu \(b\ge c\ge a\) thì đk đã cho tương đương với \(3\left(b-a\right)=5\left(b-c\right)=7\left(c-a\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}3b-3a=5b-5c\\5b-5c=7c-7a\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a+2b=5c\\7a+5b=12c\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}15a+10b=25c\\-14a-10b=-24c\end{matrix}\right.\) \(\Rightarrow a=c\). Từ đó suy ra \(a-c=0\) hay \(3\left(b-a\right)=0\Leftrightarrow a=b\). Vậy \(a=b=c\).
TH3: Nếu \(c\ge a\ge b\) thì đk đã cho tương đương với \(3\left(a-b\right)=5\left(c-b\right)=7\left(c-a\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}3a-3b=5c-5b\\5c-5b=7c-7a\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a+2b=5c\\7a-5b=2c\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}15a+10b=25c\\14a-10b=4c\end{matrix}\right.\) \(\Rightarrow29a=29c\Leftrightarrow a=c\). Từ đó suy ra \(a-c=0\) hay \(3\left(a-b\right)=0\Leftrightarrow a=b\). Vậy \(a=b=c\)
Tất cả các trường hợp còn lại làm tương tự và đều suy ra được \(a=b=c\). Ta có đpcm.

\(\dfrac{3}{5}\)\(x\) - \(\dfrac{11}{5}\) = \(\dfrac{-3}{14}\) : \(\dfrac{5}{7}\)
\(\dfrac{3}{5}\)\(x\) - \(\dfrac{11}{5}\) = - \(\dfrac{3}{10}\)
\(\dfrac{3}{5}\)\(x\) = - \(\dfrac{3}{10}\) + \(\dfrac{11}{5}\)
\(\dfrac{3}{5}\)\(x\) = \(\dfrac{19}{10}\)
\(x\) = \(\dfrac{19}{10}\) : \(\dfrac{3}{5}\)
\(x\) = \(\dfrac{19}{6}\)
\(\dfrac{3}{5}x-\dfrac{11}{5}=-\dfrac{3}{14}:\dfrac{5}{7}\)
\(\Rightarrow\dfrac{3}{5}x-\dfrac{11}{5}=-\dfrac{3}{14}\cdot\dfrac{7}{5}\)
\(\Rightarrow\dfrac{3}{5}x-\dfrac{11}{5}=-\dfrac{3}{10}\)
\(\Rightarrow\dfrac{3}{5}x=-\dfrac{3}{10}+\dfrac{11}{5}\)
\(\Rightarrow\dfrac{3}{5}x=\dfrac{19}{10}\)
\(\Rightarrow x=\dfrac{19}{10}:\dfrac{3}{5}\)
\(\Rightarrow x=\dfrac{19}{6}\)

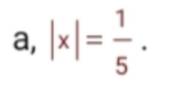
 gấp ạ
gấp ạ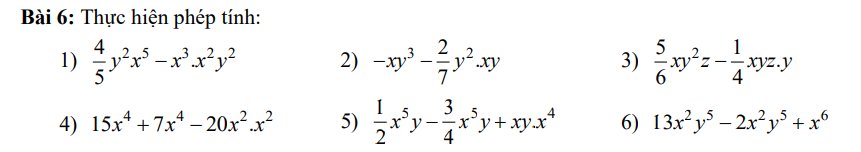 gấp ạ
gấp ạ
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.
b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)