\(x.x^2.x^3...x^{10}=3^{55}\Rightarrow x^{1+2+...10}=3^{55}\)

\(\Rightarrow x^{55}=3^{55}\Rightarrow x=3\)

(335 sửa lại thành 3⁵⁵)

\(-\dfrac{249:3}{333:3}=-\dfrac{83}{111}\Rightarrow-\dfrac{249}{333}=-\dfrac{83}{111}\)

Ta có : \(\dfrac{4a-3b}{2}=\dfrac{5b-4c}{3}=\dfrac{3c-5a}{4}\)

\(\Leftrightarrow\dfrac{20a-15b}{10}=\dfrac{15b-12c}{9}=\dfrac{12c-20a}{16}=\dfrac{20a-15b+15b-12c+12c-20a}{10+9+16}=0\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-3b=0\\5b-4c=0\\3c-5a=0\end{matrix}\right.\) 

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=\dfrac{b}{4}\\\dfrac{b}{4}=\dfrac{c}{5}\\\dfrac{c}{5}=\dfrac{a}{3}\end{matrix}\right.\Leftrightarrow\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)

 Ta thấy \(B=\left(x-1\right)\left(x-5\right)\) nên để đa thức A chia hết cho đa thức B thì \(A=\left(x-1\right)\left(x-5\right).C\) với \(C\) là một đa thức bậc 2 hệ số nguyên theo \(x\).

 Điều này tương đương với việc \(A\) có 2 nghiệm là \(x=1,x=5\). Do đó \(A\left(1\right)=0\) \(\Leftrightarrow1^4-7.1^3+10.1^2+\left(a-1\right)+b-a=0\) \(\Leftrightarrow b=-3\)

 Ta viết lại \(A=x^4-7x^3+10x^2+\left(a-1\right)x-3-a\). Ta có \(A\left(5\right)=0\) \(\Leftrightarrow5^4-7.5^3+10.5^2+\left(a-1\right).5-3-a=0\) \(\Leftrightarrow4a-8=0\) \(\Leftrightarrow a=2\).

 Vậy để đa thức A chia hết cho đa thức B thì \(a=2,b=-3\).

A:B=x2-x+11 dư (a+70)x+b-a-55

Để A chia hết cho B thì

(a+70)x+b-a-55=0

b-a-55=0 (a khác -70) tại x=0

Vậy b-a=55 thỏa đề bài

(x + 1) + (x + 2) + (x + 3) + ... + (x + 100) = 0

(x + x + x + ... + x) + (1 + 2 + 3 + ... + 100) = 0

100x + (100 + 1) . 100 : 2 = 0

100x + 5050 = 0

100x = -5050

x = -5050 : 100

x = -50,5

x = -50,5

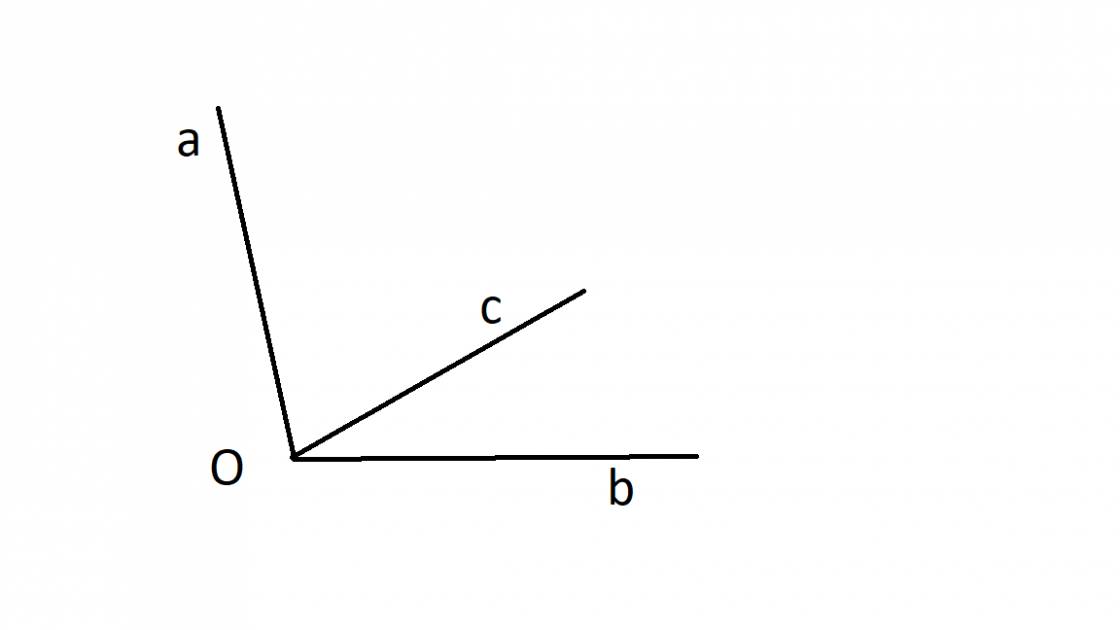Vì \(\widehat{aOc}\) và \(\widehat{cOb}\) kề bù với nhau

\(\Rightarrow\widehat{aOb}=\widehat{aOc}+\widehat{cOb}\)

\(\Leftrightarrow\widehat{aOc}=\widehat{aOb}-\widehat{cOb}\)

\(\Leftrightarrow\widehat{aOc}=100^o-30^o\)

\(\Leftrightarrow\widehat{aOc}=70^o\)

Vậy \(\widehat{aOc}=70^o\)

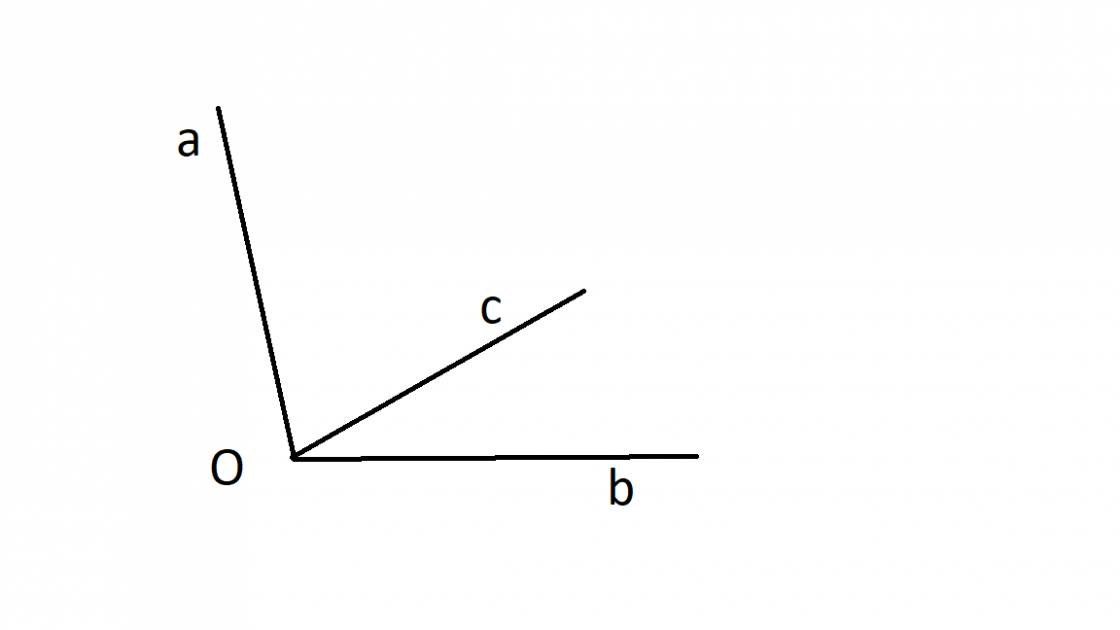
Vì góc aOc và góc cOb kề bù với nhau

=> aOb=aOc+cOb

=>aOc=aOb-cOb

<=>aOc=100^o-30^o

<=>aOc=70^o

Vậy góc aOc= 70độ