cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Chứng minh :
a) AC+BD>AB+CD
b)AC+BD>AD+ BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho mình xin phép trình bài theo kiểu lớp 8 ạ!
a) Xét ∆ABC vuông tại A có
BC=CA2+AB2(theo định lí pythagore)
<=>\(BC=\sqrt{AC^2+AB^2}\)
\(\Rightarrow BC=\sqrt{28^2+21^2}\)
\(\Rightarrow BC=35\)
Do AM là trung tuyến với cạnh BC
nên AM=BC:2
\(\Rightarrow AM=\dfrac{35}{2}\)
Mà G là trọng tâm của ∆ABC nên \(AG=\dfrac{2}{3}AM\Leftrightarrow AG=\dfrac{35}{3}\)

b,Gọi I là giao điểm của BC và ED
Xét ∆AED và ∆ABC có:
+AB=AD(gt)
+\(\widehat{BAC}=\widehat{DAB}\left(=90^o\right)\)
+AC=AE(gt)
\(\Rightarrow\)∆AED=∆ABC(ch-cgv)
\(\Rightarrow\widehat{EDA}=\widehat{ABC}\) (2 góc tương ứng)
Mà \(\widehat{DEA}+\widehat{EDA}=90^o\)( do ∆ADE vuông tại A)
\(\Rightarrow\widehat{CBA}+\widehat{DEA}=90^o\)
\(\Rightarrow\)∆BIE vuông tại I
\(\Rightarrow DE\perp BC\)

Cô làm rồi em nhé:
https://olm.vn/cau-hoi/giup-em-voiii.8161766187032

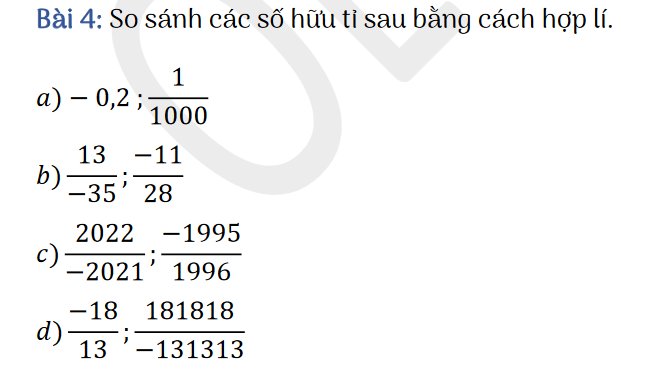
a, -0,2; \(\dfrac{1}{1000}\)
-0,2 < 0; \(\dfrac{1}{1000}\) > 0
-0,2 < \(\dfrac{1}{1000}\)
b, \(\dfrac{13}{-35}\) = \(\dfrac{-13.4}{35.4}\) = \(\dfrac{-52}{140}\); \(\dfrac{-11}{28}\) = \(\dfrac{-11.5}{28.5}\) = \(\dfrac{-55}{140}\)
vì \(\dfrac{52}{140}\) < \(\dfrac{55}{140}\)
⇒ \(\dfrac{-52}{140}\) > \(\dfrac{-55}{140}\) (khi ta nhân cả hai vế của bất đẳng thức với 1 số âm thì dấu của bất đẳng thức đổi chiều.)
Vậy \(\dfrac{13}{-35}\) > \(\dfrac{-11}{28}\)
c, \(\dfrac{2022}{-2021}\) < - 1 ; \(\dfrac{-1995}{1996}\) > -1
Vậy \(\dfrac{2022}{-2021}\) < \(\dfrac{-1995}{1996}\)
d, \(\dfrac{181818}{-131313}\) = \(\dfrac{-181818:10101}{131313:10101}\) = \(\dfrac{-18}{13}\)
vậy \(\dfrac{-18}{13}\) = \(\dfrac{181818}{-131313}\)

a,b \(\in\) Z, a \(\ne\) b, b > 0
So sánh: \(\dfrac{a}{b}\) và \(\dfrac{a+2022}{b+2022}\)
Có hai trường hợp:
+ Nếu a < b ta có:
\(\dfrac{a}{b}\) = 1 - \(\dfrac{b-a}{b}\) ; \(\dfrac{a+2022}{b+2022}\) = 1 - \(\dfrac{b-a}{b+2022}\)
Vì \(\dfrac{b-a}{b}\) > \(\dfrac{b-a}{b+2022}\)
Vậy : \(\dfrac{a}{b}\) < \(\dfrac{a+2022}{b+2022}\)
+ Nếu a > b ta có
\(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b}\); \(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b+2022}\)
Vì \(\dfrac{a-b}{b}\) > \(\dfrac{a-b}{b+2022}\)
Vậy \(\dfrac{a}{b}\) > \(\dfrac{a+2022}{b+2022}\)

a) \(\dfrac{x}{3}=\dfrac{-10}{6}\)
\(x\times6=-10\times3\)
\(x\times6=-30\)
\(x=-5\)
b) \(\dfrac{-8}{x}=\dfrac{-9}{15}\)
\(x\times-9=15\times-8\)
\(x\times-9=-120\)
\(x=\dfrac{40}{3}\)
c) \(\dfrac{2,7}{0,9}=\dfrac{-8}{x}\)
\(x\times2,7=-8\times0,9\)
\(x\times2,7=-7,2\)
\(x=-\dfrac{8}{3}\)
d) \(\dfrac{4}{9}=\dfrac{x}{12}\)
\(x\times9=12\times4\)
\(x\times9=48\)
\(x=\dfrac{48}{9}\)
\(x=\dfrac{16}{3}\)


Số liệu đó đã được làm tròn đến hàng trăm triệu em nhé.
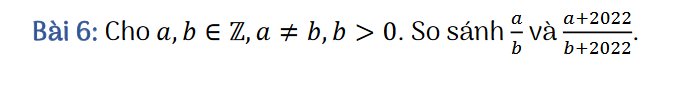
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD