Mn ơi nếu bài toán thực tế nó kêu làm tròn đến hàng đơn vị thì e xuống phần kết luận làm tròn được không ạ !!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(mx+7=6\) (1) (m ≠ 0)
\(\Leftrightarrow mx=-1\)
\(\Leftrightarrow x=\frac{-1}{m}\)
Lại có: \(\frac{x}{2}+m=1\) (2)
\(\Leftrightarrow \frac{x}{2}=1-m\)
\(\Leftrightarrow x=2-2m\)
Để 2 phương trình (1) và (2) có nghiệm bằng nhau thì:
\(\frac{-1}{m}=2-2m\\\Leftrightarrow2m-2-\frac{1}{m}=0\\\Leftrightarrow 2m^2-2m-1=0(\text{vì }m\ne0)\\\Leftrightarrow \left[\begin{array}{} m=\frac{1+\sqrt3}{2}(tmdk)\\ m=\frac{1-\sqrt3}{2}(tmdk) \end{array} \right. \)
$\text{#}Toru$
Ta có pt(1):
\(mx+7=6\left(m\ne0\right)\)
\(\Leftrightarrow mx=6-7=-1\)
\(\Leftrightarrow x=-\dfrac{1}{m}\)
Pt(2) \(\dfrac{x}{2}+m=1\)
\(\Leftrightarrow\dfrac{x}{2}=1-m\)
\(\Leftrightarrow x=2\left(1-m\right)=2-2m\)
Vì 2 phương trình có nghiệm bằng nhau nên:
\(-\dfrac{1}{m}=2-2m\)
\(\Leftrightarrow-1=m\left(2-2m\right)\)
\(\Leftrightarrow-1=2m-2m^2\)
\(\Leftrightarrow2m^2-2m-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1+\sqrt{3}}{2}\\m=\dfrac{1-\sqrt{3}}{2}\end{matrix}\right.\left(tm\right)\)
Vậy: ...

Ta có pt(1): \(mx+7=6\left(m\ne0\right)\)
\(\Leftrightarrow mx=6-7\)
\(\Leftrightarrow mx=-1\)
\(\Leftrightarrow x=-\dfrac{1}{m}\)
pt(2): \(\dfrac{x}{2+m}=1\left(m\ne-2\right)\)
\(\Leftrightarrow x=1\cdot\left(2+m\right)=m+2\)
Vì 2 pt có 2 nghiệm bằng nhau nên ta có:
\(-\dfrac{1}{m}=m+2\)
\(\Leftrightarrow-1=m\left(m+2\right)\)
\(\Leftrightarrow-1=m^2+2m\)
\(\Leftrightarrow m^2+2m+1=0\)
\(\Leftrightarrow\left(m+1\right)^2=0\)
\(\Leftrightarrow m+1=0\)
\(\Leftrightarrow m=-1\left(tm\right)\)
Vậy: ...


\(xy< =\dfrac{x^2+y^2}{2}\)
=>\(xy< =\dfrac{2}{2}=1\)
=>xy+1<=2
Dấu '=' xảy ra khi xy=1
=>\(x=\dfrac{1}{y}\)
\(\left(x+y\right)\left(1+xy\right)^3=16\)
=>\(\left(y+\dfrac{1}{y}\right)\left(1+1\right)^3=16\)
=>\(y+\dfrac{1}{y}=2\)
=>y=1
=>x=1

Gọi chiều rộng là x(m)
(Điều kiện: x>0)
Chiều dài là x+2(m)
Diện tích là 80m2 nên x(x+2)=80
=>\(x^2+2x-80=0\)
=>(x+10)(x-8)=0
=>\(\left[{}\begin{matrix}x=-10\left(nhận\right)\\x=8\left(nhận\right)\end{matrix}\right.\)
Chiều dài là 8+2=10(m)
Chu vi là \(\left(8+10\right)\cdot2=36\left(m\right)\)
Gọi chiều dài của HCN là x (m)
ĐK: x>0
Chiều rộng là: \(x-2\left(m\right)\)
HCN có diện tích là 80 `m^2` nên ta có pt:
\(x\left(x-2\right)=80\)
\(\Leftrightarrow x^2-2x-80=0\)
\(\Leftrightarrow x^2-10x+8x-80=0\)
\(\Leftrightarrow x\left(x-10\right)+8\left(x-10\right)=0\Leftrightarrow\left(x+8\right)\left(x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-8\left(ktm\right)\\x=10\left(tm\right)\end{matrix}\right.\)
Chiều rộng HCN là: \(10-2=8\left(m\right)\)
Chu vi HCN là: `(10+8) xx 2 = 36 (m)`

A = \(x^2\) + 5\(x\) - 6
A = \(x^2\) - \(x\) + 6\(x\) - 6
A = (\(x^2\) - \(x\)) + (6\(x\) - 6)
A = \(x\).(\(x-1\)) + 6.(\(x-1\))
A = (\(x\) - 1).(\(x\) + 6)

chưa được nha bạn
phải ghi rõ thế này nè: AB=AC
=>A nằm trên đường trung trực của BC(1)
OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
Cái này mới được điểm!

\(\left\{{}\begin{matrix}\left(x-1\right)\left(2y+1\right)=\left(x-3\right)\left(y-5\right)+xy\\\left(x+1\right)\left(y+1\right)=\left(2x-1\right)\left(y+1\right)-xy\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2xy+x-2y-1=xy-5x-3y+15+xy\\xy+x+y+1=2xy+2x-y-1-xy\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-2y-1=-5x-3y+15\\x+y+1=2x-y-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x+y=16\\-x+2y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x+2y=32\\-x+2y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}13x=34\\6x+y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{34}{13}\\y=16-6x=16-6\cdot\dfrac{34}{13}=\dfrac{4}{13}\end{matrix}\right.\)
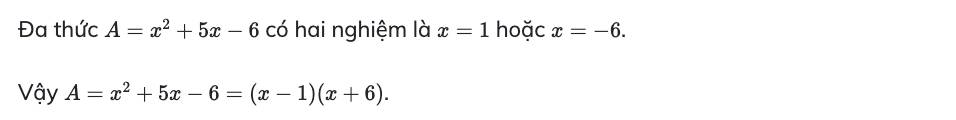


Theo mình thì được bạn nhé!
Chắc đc bạn ạ !