x^2-4x-3=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi 2 số chính phương đó là: \(a^2\) và \(b^2\)
Ta có:
\(n=a^2+b^2\)
\(n^2=a^4+2\left(ab\right)^2+b^4\)
\(n^2=\left(a^4-2\left(ab\right)^2+b^4\right)+4\left(ab\right)^2\)
\(n^2=\left(a^2-b^2\right)^2+\left(2ab\right)^2\left(đpcm\right)\)

Đặt \(2021=a\)
\(a^2+\left(a+1\right)^2+\left(a+2\right)^2\)
\(=3a^2+6a+5\)
\(=3\left(a^2+2a+1\right)+2\)
\(=3\left(a+1\right)^2+2\) không là số chính phương
2021 \(\equiv\) 5 (mod 8) 2022 \(\equiv\) 6 (mod 8)
20212 \(\equiv\) 25 (mod 8) 20222 \(\equiv\) 36 (mod 8)
25 \(\equiv\) 1 (mod 8) 36 \(\equiv\) 4 (mod 8)
20212 \(\equiv\) 1 (mod 8) 20222 \(\equiv\) 4 (mod 8)
2023 \(\equiv\) -`1 (mod 8)
20232 \(\equiv\) 1 (mod 8)
20212 + 20222 + 20232 \(\equiv\) 1 + 1 + 4 (mod 8)
20212 + 20222 + 20232 \(\equiv\) 6 (mod 8)
\(\Rightarrow\) 20212 + 20222 + 20232 không phải là số chính phương vì một số chính phương chia 8 chỉ có thể dư 0; 1 hoặc 4


\(A=x\left(x-3\right)\left(x-4\right)\left(x-7\right)=\left(x^2-7x\right)\left(x^2-7x+12\right)=\left(x^2-7x+6\right)^2-36\)
\(\forall x\Rightarrow\left(x^2-7x+6\right)\ge0\Rightarrow\left(x^2-7x+6\right)^2-36\ge-36\)
\(\Rightarrow A_{min}=-36\Leftrightarrow x=1\) hoặc \(x=6\)
\(B=\dfrac{2}{6x-5-9x^2}\)
\(6x-5-9x^2=-\left(9x^2-6x+1\right)-4=-4-\left(3x-1\right)^2\le-4\)
\(\Rightarrow B\ge\dfrac{2}{-4}=\dfrac{-1}{2}\)
\(\Rightarrow B_{min}=\dfrac{-1}{2}\Leftrightarrow x=\dfrac{1}{3}\)
\(C=\dfrac{3x^2-8x+6}{\left(x-1\right)^2}=\dfrac{3\left(x-1\right)^2-2x+3}{\left(x-1\right)^2}=3+\dfrac{-2\left(x-1\right)+1}{\left(x-1\right)^2}\)
\(=\dfrac{1}{\left(x-1\right)^2}-\dfrac{2}{x-1}+3=\left(\dfrac{1}{x-1}-1\right)^2+2\ge2\)
\(C_{min}=2\Leftrightarrow x=2\)

Nhìn biểu thức rối quá. Bạn cần viết lại bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

Áp dụng bất đẳng thức cosi có :
\(\sqrt{3a\left(a+2b\right)}\le\dfrac{3a+a+2b}{2}=2a+b\)
=> \(a\sqrt{3a\left(a+2b\right)}\le2a^2+ab\) (1)
Tương tự \(b\sqrt{3b\left(b+2a\right)}\) \(\le2b^2+ab\) (2)
Từ (1);(2) => \(a\sqrt{3a\left(a+2b\right)}+b\sqrt{3b\left(b+2a\right)}\le2a^2+2b^2+2ab\) \(\le2a^2+2b^2+a^2+b^2=3\left(a^2+b^2\right)\le6\)
Xấu '=' xảy ra khi a=b=1

Gọi số tự nhiên chẵn ở giữa là a ( \(a\inℕ^∗\) ; a >2 )
=> Ba số tự nhiên chẵn liên tiếp sẽ là a - 2 ; a và a + 2
Vì tích 2 số sau lớn hơn tích 2 số đầu là 24
=> Ta có phương trình
\(a\left(a-2\right)+24=a\left(a+2\right)\)
\(\Leftrightarrow a^2-2a+24=a^2+2a\)
\(\Leftrightarrow\text{4a = 24 suy ra a = 6 ( TM ) }\)
=> Ba số cần tìm là 4 ; 6 và 8
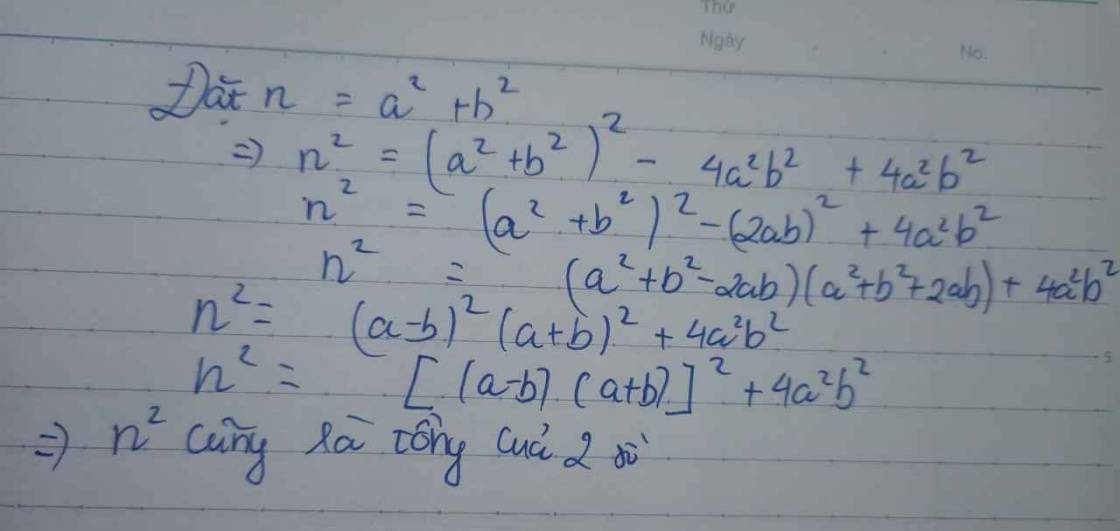

`x^2-4x-3=0`
`<=>x^2-4x+4-7=0`
`<=>(x-2)^2=7`
`<=>|x-2|=\sqrt{7}`
`<=>x=2+-\sqrt{7}`
Vậy `S={2+-\sqrt{7}}`