cho a tỉ lệ thuận với b theo hệ số tỉ lệ k1=5 . B tỉ lệ thuận với c theo hệ số tỉ lệ k2=7 . Chứng tỏ a tỉ lêj thuận với c và chỉ ra hệ số tỉ lệ k
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Sau khi chạy hết một còng chiều dài đoạn đường chạy mà vận động viên đã hoàn thành là :
\(\left(64+109\right)\times2=346\left(m\right)\)
Vậy............
Số m chiều dài đoạn đường chạy mà vđv đã hoàn thành 1 vòng :
\(\left(64+109\right).2=346\left(m\right)\)
Đáp số...

Lời giải:
a. $=\frac{1}{2}+\frac{3}{16}+\frac{3}{4}$
$=\frac{8}{16}+\frac{3}{16}+\frac{12}{16}$
$=\frac{8+3+12}{16}=\frac{23}{16}$
b.
$=\frac{2}{3}-2+\frac{1}{3}+\frac{3}{2}+1$
$=(\frac{2}{3}+\frac{1}{3})+\frac{3}{2}-2+1$
$=1+\frac{3}{2}-2+1=2-2+\frac{3}{2}=\frac{3}{2}$
c.
$=\frac{5}{4}-\frac{5}{6}:\frac{5}{24}+\frac{11}{12}$
$=\frac{5}{4}-4+\frac{11}{12}=(\frac{5}{4}+\frac{11}{12})-4=\frac{13}{6}-4=\frac{-11}{6}$
d.
$=\frac{2}{3}+(-1,5):1,5=\frac{2}{3}+(-1)=\frac{-1}{3}$

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$
Khi đó:
$\frac{2a+3b}{3a-5b}=\frac{2bk+3b}{3bk-5b}=\frac{b(2k+3)}{b(3k-5)}=\frac{2k+3}{3k-5}(1)$
$\frac{2c+3d}{3c-5d}=\frac{2dk+3d}{3dk-5d}=\frac{d(2k+3)}{d(3k-5)}=\frac{2k+3}{3k-5}(2)$
Từ $(1); (2)$ ta có đpcm.

a) \(...=P\left(x\right)=2x^4-x^4+3x^3+4x^2-3x^2+3x-x+3\)
\(P\left(x\right)=x^4+3x^3+x^2+2x+3\)
\(...=Q\left(x\right)=x^4+x^3+3x^2-x^2+4x+4-2\)
\(Q\left(x\right)=x^4+x^3+2x^2+4x+2\)
b) \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)+\left(x^4+x^3+2x^2+4x+2\right)\)
\(\Rightarrow P\left(x\right)+Q\left(x\right)=2x^4+4x^3+3x^2+6x+5\)
\(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)-\left(x^4+x^3+2x^2+4x+2\right)\)
\(\)\(\Rightarrow P\left(x\right)-Q\left(x\right)=x^4+3x^3+x^2+2x+3-x^4-x^3-2x^2-4x-2\)
\(\Rightarrow P\left(x\right)-Q\left(x\right)=2x^3-x^2-2x+1\)

\(\dfrac{-3}{26}+2\dfrac{4}{69}\)
\(=\dfrac{-3}{26}+\dfrac{142}{69}\)
\(=\dfrac{-3.69}{26.69}+\dfrac{142.26}{26.69}\)
\(=\dfrac{-207+3692}{1794}\)
\(=\dfrac{3485}{1794}\)
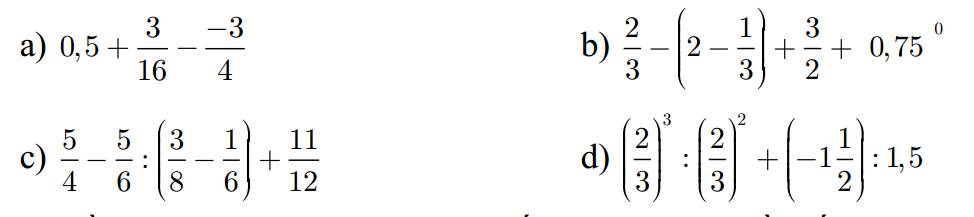
\(\dfrac{a}{b}=k_1=5\)
\(\dfrac{b}{c}=k_2=7\)
\(\Rightarrow\dfrac{a}{b}.\dfrac{b}{c}=\dfrac{a}{c}=k_1.k_2=5.7=35\)
\(\Rightarrow\dfrac{a}{c}=k=35\)