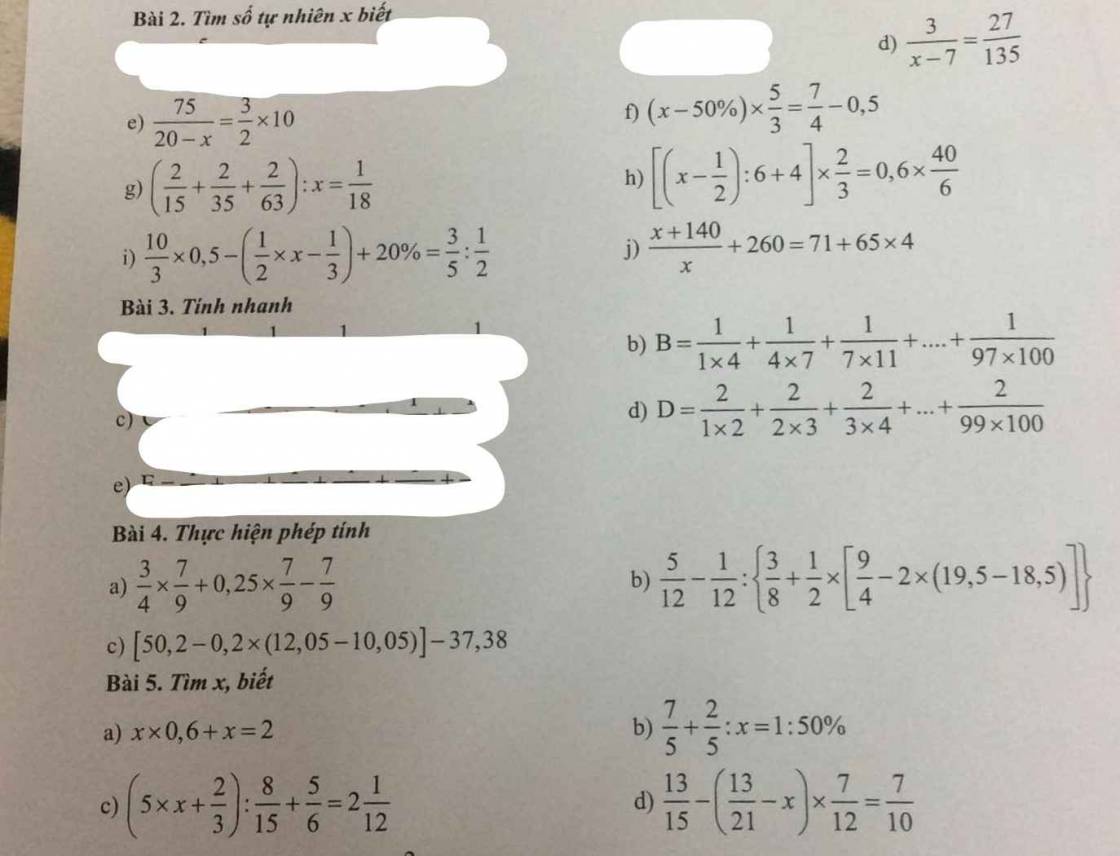
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1}{5}\sqrt[]{25x+50}-5\sqrt[]{x+2}+\sqrt[]{9x+18}+9=0\)
\(\Leftrightarrow\dfrac{1}{5}\sqrt[]{25\left(x+2\right)}-5\sqrt[]{x+2}+\sqrt[]{9\left(x+2\right)}+9=0\)
\(\Leftrightarrow\dfrac{1}{5}.5\sqrt[]{x+2}-5\sqrt[]{x+2}+3\sqrt[]{x+2}+9=0\)
\(\Leftrightarrow\sqrt[]{x+2}-5\sqrt[]{x+2}+3\sqrt[]{x+2}+9=0\)
\(\Leftrightarrow\sqrt[]{x+2}\left(1-5+3\right)+9=0\)
\(\Leftrightarrow-\sqrt[]{x+2}+9=0\)
\(\Leftrightarrow\sqrt[]{x+2}=9\)
\(\Leftrightarrow x+2=81\)
\(\Leftrightarrow x=79\)



\(\dfrac{1}{2}.x+0,4.\left(x-1\right)=0\)
\(\dfrac{1}{2}.x+0,4.x-0,4=0\)
\(\dfrac{1}{2}.x+0,4.x=0+0,4\)
\(\dfrac{1}{2}.x+0,4.x=0,4\)
\(x.\left(\dfrac{1}{2}+0,4\right)=0,4\)
\(x.\left(0,5+0,4\right)=0,4\)
\(x.0,9=0,4\)
\(x=0,4:0,9\)
\(x=\dfrac{4}{9}\)

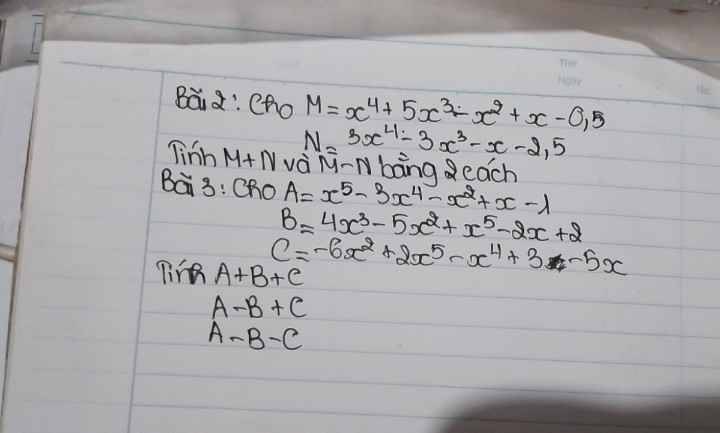
Bài 4: Thực hiện phép tính:
a, \(\dfrac{3}{4}\) \(\times\) \(\dfrac{7}{9}\) + 0,25 \(\times\) \(\dfrac{7}{9}\) - \(\dfrac{7}{9}\)
= \(\dfrac{7}{9}\) (0,75 + 0,25 - 1)
= 0
b, \(\dfrac{5}{12}\) - \(\dfrac{1}{12}\): (\(\dfrac{3}{8}\) + \(\dfrac{1}{2}\).[\(\dfrac{9}{4}\) - 2.(19,5 -18,5)])
= \(\dfrac{5}{12}\) - \(\dfrac{1}{12}\): ( \(\dfrac{3}{8}\) + \(\dfrac{1}{2}\). [ \(\dfrac{9}{4}\)- 2])
= \(\dfrac{5}{12}\) - \(\dfrac{1}{12}\): ( \(\dfrac{3}{8}\) + \(\dfrac{9}{8}\)- 1)
= \(\dfrac{5}{12}\) - \(\dfrac{1}{12}\): ( \(\dfrac{1}{2}\))
= \(\dfrac{5}{12}\) - \(\dfrac{1}{6}\)
= \(\dfrac{1}{4}\)
c, [ 50,2 - 0,2 .(12,05 - 10,05)] - 37,38
= [ 50,2 - 0,2. 2 ] - 37,38
= [ 50,2 - 0,4] - 37,38
= 49,8 - 37,38
= 12,42
Bài 3:
B = \(\dfrac{1}{1.4}\)+\(\dfrac{1}{4.7}+\dfrac{1}{7.11}+...+\dfrac{1}{97.100}\)
B = \(\dfrac{1}{3}\).( \(\dfrac{3}{1.4}\)+ \(\dfrac{3}{4.7}\)+ \(\dfrac{3}{7.11}\)+...+ \(\dfrac{3}{97.100}\))
B = \(\dfrac{1}{3}\).( \(\dfrac{1}{1}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{7}\)+ \(\dfrac{1}{7}\) - \(\dfrac{1}{11}\) +...+ \(\dfrac{1}{97}\) - \(\dfrac{1}{100}\))
B = \(\dfrac{1}{3}\).( \(\dfrac{1}{1}\) - \(\dfrac{1}{100}\))
B = \(\dfrac{1}{3}\). \(\dfrac{99}{100}\)
B = \(\dfrac{33}{100}\)