chưa ai giúp bạn sao : olm tới rồi!

C = \(\overline{44444.......44}\)  (n chữ số 4)

C = 4. \(\overline{11111.....111}\) ( chữ số 1)

giả sử C là một số chính phương thì 

⇔ 4. \(\overline{1111.......111}\) là một số chính phương 

vì 4 là một số chính phương nên 

⇔ \(\overline{11111.....111}\) là một số chính phương 

một số chính phương có tận cùng là 1 thì chữ số hàng chục phải là chữ số chẵn. mà \(\overline{1111.....111}\) lại có chữ số hàng chục là chữ số lẻ nên \(\overline{111....111}\) là một số chính phương là sai . dẫn đến điều giả sử là sai .

vậy C = \(\overline{44444...444}\) không phải là một số chính phương (đpcm)

lấy n = 2, ta thấy 44 không phải là số chính phương.

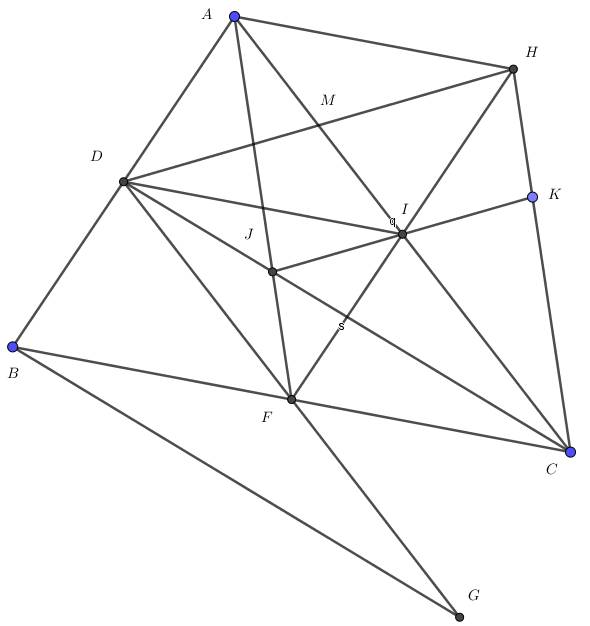
a) Xét △ABC có:

DA = DB (gt)

FB = FC (gt)

=> DF là đường trung bình của △ABC

=> DF // AC

Xét tứ giác ADFC có:

DF // AC (cmt)

=> Tứ giác ADFC là hình thang

b) Ở câu này đề bài cho bị thiếu △ABC cân tại B, vì nếu không có yếu tối này thì AF không thể bằng BG được.                                                                                                                                                             c)  Xét tứ giác ABFH có:

AB // FH

AH // BF

=> Tứ giác ABFH là hình bình hành 

=> AH = BF mà BF = FC 

=> AH = FC

Xét tứ giác AHCF có:

AH // CF

AH = CF

=> AHCF là hình bình hành

=> AF // CH

d) Gọi M là giao điểm của AI và DH

Xét tứ giác ADIH có:

AD // IH

AH // DI

=> Tứ giác ADIH là hình bình hành

=> M là trung điểm của AI hay IM = \(\dfrac{1}{2}AI\)

mà AI =  IC ( vì AHCF là hình bình hành)

=> IM = \(\dfrac{1}{2}IC\) =>IM=\(\dfrac{1}{3}MC\)   

Xét △CHM có:

HK = \(\dfrac{1}{3}HC\)

IM=\(\dfrac{1}{3}MC\)             

=> IK // MH ( định lý đảo Ta-lét)

hay IK // DH (1)

Xét △ABC có:

AF, CD là trung tuyến

mà AF cắt CD tại J => J là trọng tâm của  △ABC

=> DJ = \(\dfrac{1}{3}DC\)              

Xét △DHC có:

 HK = \(\dfrac{1}{3}HC\)   

  DJ = \(\dfrac{1}{3}DC\)    

=> JK // DH (2)

Từ (1) và (2) theo tiên đề Ơ-lít ta có: J, I, K thẳng hàng.                                            

x³ + 4x² - 7x - 10 = 0

x³ + 5x²  - x² - 5x - 2x - 10 = 0

 x² . ( x + 5 ) - x . ( x + 5 ) - 2 . ( x + 5 ) = 0

     ( x + 5 ) . ( x² - x - 2 ) = 0 

         ( x + 5 ) . ( x² - 2x + x - 2 ) = 0

             ( x + 5 ) . ( x + 1 ) . ( x - 2 )  = 0

   đến đây dễ rồi tự tính đi =) :33

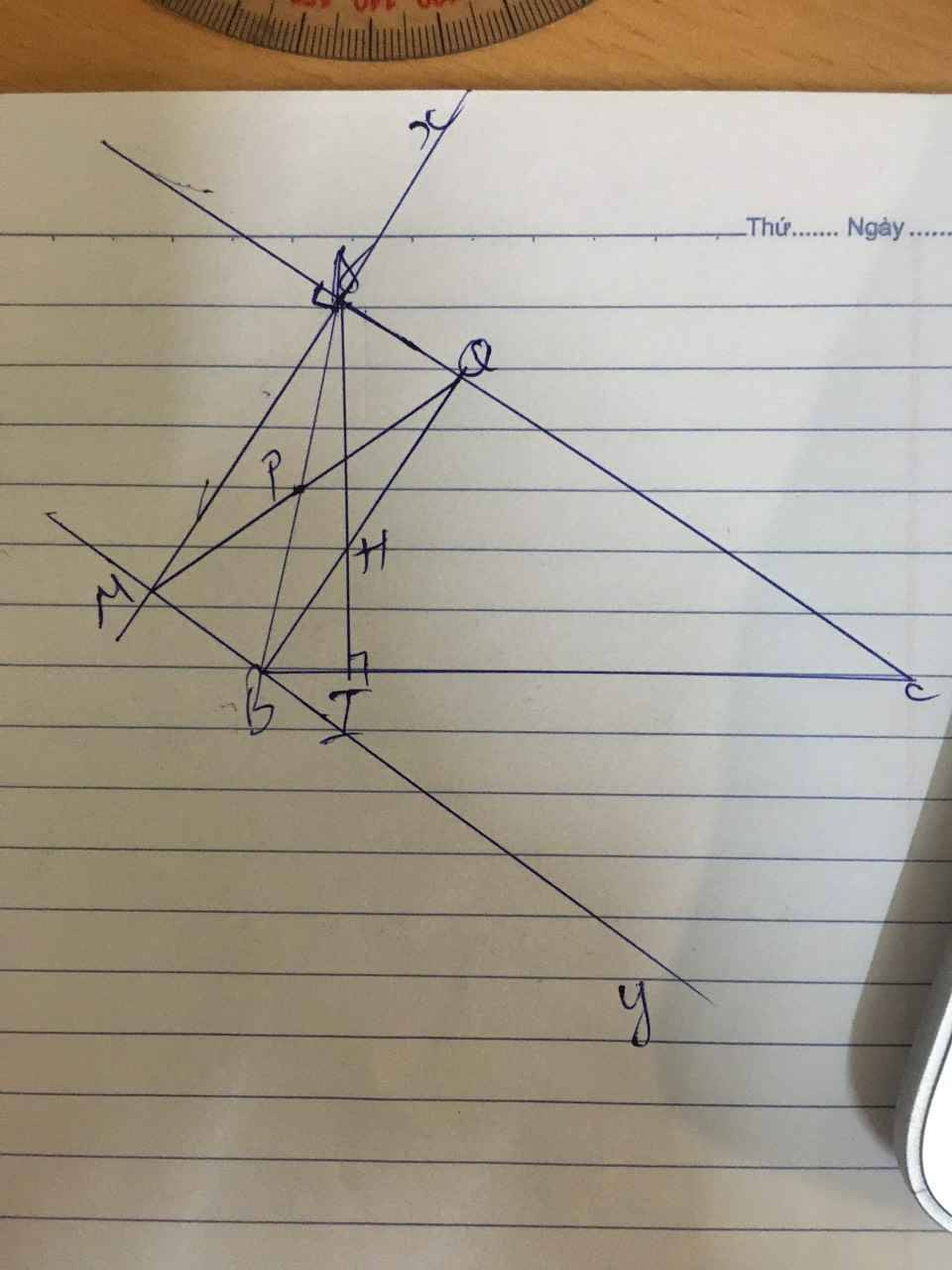
a) tứ giác AMPQ là hcn

b) ta có Ax \(\perp\) AC (gt)

M là giao điểm Ax và By ⇒ M ϵ Ax và M ϵ By

⇒ AM \(\perp\) AC

có BM // AC ⇒ AM\(\perp BM\)

xét △ APQ = △ BPM (gcg) ⇒ AQ = MB 

xét tứ giác AQBM có AQ //MB; AQ = MB; AM\(\perp BM\)

⇒ AQBM là hcn 

⇒ BQ \(\perp\)AC 

xét △ ABC có AI, BQ là đường cao cắt nhau tại H ⇒ H là trực tâm của △ABC ⇒ CH \(\perp AB\)

c) xét △ vuông AIB có P là trung điểm AB ⇒ IP =AP = PB 

mà AP = PB = PQ = MP( tc đường chéo của hcn)

⇒  IP = PQ ⇒ △ IPQ cân tại P