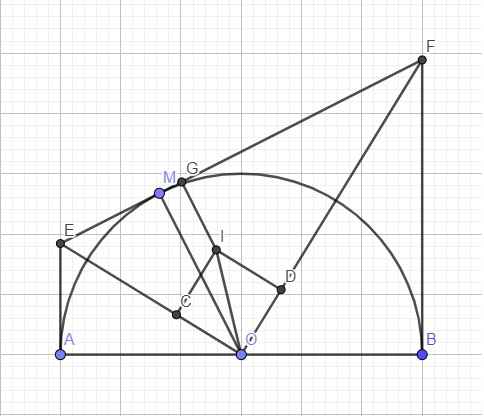
Câu 5 (4 điêm): Cho đường tròn (O) Từ một đièm A ờ ngoài đường tròn, vẻ tiếp tuyên AB ; AC và cát tuyên ADE sao cho tia AD nam giữa hai tia AO x á AC (AD < AE) gọi H là trung điêm của DE. BM là đường kinh
a) Chứng minh tó giác ABOH là tứ giác nội tièp
b) Chứng minh tứ giác AOMC là hình thang
c) Qua E kẽ đường thăng song song x ới AO cat BM tại K Chứng minh HK//DM
d) Tia MD cat AO tai p. EO cat BP tại F ; Chứng mmh F thuộc (O)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi năng suất dự định của tổ SX là \(x\left(sp/h\right)\)\(\left(x\in N;0< x\le20\right)\)
Thời gian dự định để tổ hoàn thành công việc là \(\frac{72}{x}\left(h\right)\)
Năng suất thực tế của đội là \(x+1\left(sp/h\right)\)
Thời gian thực tế tổ đã dành ra để hoàn thành công việc là \(\frac{80}{x+1}\left(h\right)\)
VÌ thời gian thực tế chậm hơn dự định 12p nên ta có pt \(\frac{80}{x+1}-\frac{72}{x}=\frac{1}{5}\)\(\Leftrightarrow\frac{80x-72x-72}{\left(x+1\right)x}=\frac{1}{5}\)\(\Leftrightarrow\frac{8x-72}{x^2+x}=\frac{1}{5}\)\(\Rightarrow x^2+x=40x-360\)\(\Leftrightarrow x^2-39x+360=0\)(*)
pt (*) có \(\Delta=\left(-39\right)^2-4.360=81>0\)\(\Rightarrow\)pt (*) có 2 nghiệm phân biệt \(\orbr{\begin{cases}x_1=\frac{-\left(-39\right)+\sqrt{81}}{2}=24\left(loại\right)\\x_2=\frac{-\left(-39\right)-\sqrt{81}}{2}=15\left(nhận\right)\end{cases}}\)
Vậy năng suất dự định cửa tổ SX là 15 sp/h

Ta có : Hệ \(\hept{\begin{cases}x^3+xy^2-10y=0\\x^2+6y^2=10\end{cases}}\Leftrightarrow\hept{\begin{cases}x\left(x^2+y^2\right)-10y=0\\x^2+6y^2=10\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x\left(10-6y^2+y^2\right)-10y=0\\x^2=10-6y^2\end{cases}\Leftrightarrow\hept{\begin{cases}2x-xy^2-2y=0\\x^2=10-6y^2\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{2y}{2-y^2}\\x^2=10-6y^2\end{cases}}\)(1)
Với y = \(\pm\sqrt{2}\)=> \(∄\)x thỏa mãn hệ
=> y \(\ne\pm\sqrt{2}\)
Khi đó hệ (1) <=> \(\hept{\begin{cases}\left(\frac{2y}{2-y^2}\right)^2=10-6y^2\\x^2=10-6y^2\end{cases}}\Leftrightarrow\hept{\begin{cases}6y^6-34y^4+68y^2-40=0\left(2\right)\\x^2=10-6y^2\left(^∗\right)\end{cases}}\)
Đặt t = y2 \(\ge0\)
Khi đó (2) <=> 6t3 - 34t2 + 68t - 40 = 0
<=> 3t3 - 17t2 + 34t - 20 = 0
<=> (3t3 - 3) - 17(t2 - 2t + 1) = 0
<=> 3(t - 1)(t2 + t + 1) - 17(t - 1)2 = 0
<=> (t - 1)(3t2 - 14t + 20) = 0
<=> t - 1 = 0 (Vì 3t2 - 14t + 20 > 0 \(\forall t\))
<=> t = 1
Khi đó y2 = 1 <=> y = \(\pm1\)
Thay y = \(\pm1\)vào (*)
=> x2 = 10 - 6y2 = 10 - 6 = 4 <=> x = \(\pm2\)
Vậy hệ có 4 nghiệm (2 ; 1) ; (2 ; - 1) ; (-2 ; - 1) ; (-2 ; 1)
\(\Rightarrow x^3+xy^2-\left(x^2+6y^2\right)y=0\)
\(\Leftrightarrow x^3-x^2y+xy^2-6y^3=0\)
\(\Leftrightarrow\left(x-2y\right)\left(x^2+xy+3y^2\right)=0\)
\(\Rightarrow x=2y\)
Thế vào \(x^2+6y^2=10\)
\(\Rightarrow10y^2=10\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-1\Rightarrow x=-2\end{matrix}\right.\)

ĐKXĐ: \(x\ne-1;y\ne2\)
\(\left\{{}\begin{matrix}\dfrac{3}{x+1}-\dfrac{4}{y-2}+1=0\\x+1+y-2=2\left(x+1\right)\left(y-2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{3}{x+1}-\dfrac{4}{y-2}=-1\\\dfrac{1}{x+1}+\dfrac{1}{y-2}=2\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+1}=u\\\dfrac{1}{y-2}=v\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3u-4v=-1\\u+v=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u=1\\v=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}=1\\\dfrac{1}{y-2}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x+1=1\\y-2=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=0\\y=3\end{matrix}\right.\)

\(\left(a^2+\dfrac{1}{b^2}\right)\left(\dfrac{1}{4}+4\right)\ge\left(\dfrac{a}{2}+\dfrac{2}{b}\right)^2\)
\(\Rightarrow\sqrt{a^2+\dfrac{1}{b^2}}\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{a}{2}+\dfrac{2}{b}\right)\)
Tương tự: \(\sqrt{b^2+\dfrac{1}{c^2}}\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{b}{2}+\dfrac{2}{c}\right)\) ; \(\sqrt{c^2+\dfrac{1}{a^2}}\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{c}{2}+\dfrac{2}{a}\right)\)
Cộng vế:
\(S\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{a+b+c}{2}+\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}\right)\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{a+b+c}{2}+\dfrac{18}{a+b+c}\right)\)
\(S\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{a+b+c}{2}+\dfrac{9}{8\left(a+b+c\right)}+\dfrac{135}{8\left(a+b+c\right)}\right)\)
\(S\ge\dfrac{2}{\sqrt{17}}\left(2\sqrt{\dfrac{9\left(a+b+c\right)}{16\left(a+b+c\right)}}+\dfrac{135}{8.\dfrac{3}{2}}\right)=\dfrac{3\sqrt{17}}{2}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)

Cách 1:
Do vai trò của a;b;c là như nhau, không mất tính tổng quát, giả sử \(a\ge b\ge c\)
\(\Rightarrow3=ab+bc+ca\le3ab\Rightarrow ab\ge1\)
Ta có:
\(\dfrac{1}{1+a^2}+\dfrac{1}{1+b^2}=\dfrac{a^2+b^2+2}{a^2b^2+a^2+b^2+1}=1-\dfrac{a^2b^2-1}{a^2b^2+a^2+b^2+1}\)
\(\ge1-\dfrac{a^2b^2-1}{a^2b^2+2ab+1}=1-\dfrac{ab-1}{ab+1}=\dfrac{2}{1+ab}\)
\(\Rightarrow VT\ge\dfrac{2}{1+ab}+\dfrac{1}{1+c^2}\)
Nên ta chỉ cần chứng minh:
\(\dfrac{2}{1+ab}+\dfrac{1}{1+c^2}\ge\dfrac{3}{2}\Leftrightarrow c^2+3-ab\ge3abc^2\)
\(\Leftrightarrow c^2+ac+bc\ge3abc^2\Leftrightarrow a+b+c\ge3abc\)
\(\Leftrightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\ge3\)
Đúng do \(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\ge\dfrac{9}{ab+bc+ca}=3\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Cách 2:
\(\Leftrightarrow1-\dfrac{a^2}{a^2+1}+1-\dfrac{b^2}{b^2+1}+1-\dfrac{c^2}{c^2+1}\ge\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{3a^2}{3a^2+3}+\dfrac{3b^2}{3b^2+3}+\dfrac{3c^2}{3c^2+3}\le\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{3a^2}{2a^2+a^2+ab+bc+ca}+\dfrac{3b^2}{2b^2+b^2+ab+bc+ca}+\dfrac{3c^2}{2c^2+c^2+ab+bc+ca}\le\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{a^2}{a\left(a+b+c\right)+2a^2+bc}+\dfrac{b^2}{b\left(a+b+c\right)+2b^2+ac}+\dfrac{c^2}{c\left(a+b+c\right)+2c^2+ab}\le\dfrac{1}{2}\)
Ta có:
\(\dfrac{a^2}{a\left(a+b+c\right)+2a^2+bc}\le\dfrac{1}{4}\left(\dfrac{a^2}{a\left(a+b+c\right)}+\dfrac{a^2}{2a^2+bc}\right)=\dfrac{1}{4}\left(\dfrac{a}{a+b+c}+\dfrac{a^2}{2a^2+bc}\right)\)
Tương tự và cộng lại:
\(VT\le\dfrac{1}{4}\left(1+\dfrac{a^2}{2a^2+bc}+\dfrac{b^2}{2b^2+ac}+\dfrac{c^2}{2c^2+ab}\right)\)
Nên ta chỉ cần chứng minh:
\(\dfrac{a^2}{2a^2+bc}+\dfrac{b^2}{2b^2+ac}+\dfrac{c^2}{2c^2+ab}\le1\)
\(\Leftrightarrow\dfrac{bc}{2a^2+bc}+\dfrac{ac}{2b^2+ac}+\dfrac{ab}{2c^2+ab}\ge1\)
\(\Leftrightarrow\dfrac{\left(bc\right)^2}{2a^2bc+\left(bc\right)^2}+\dfrac{\left(ca\right)^2}{2ab^2c+\left(ac\right)^2}+\dfrac{\left(ab\right)^2}{2abc^2+\left(ab\right)^2}\ge1\)
Đúng do:
\(VT\ge\dfrac{\left(ab+bc+ca\right)^2}{\left(ab+bc+ca\right)^2}=1\)

Gọi I là tâm đường tròn nội tiếp EOF, C và D lần lượt là tiếp điểm của (I) với OE và OF
Tứ giác ICOD là hình chữ nhật (có 3 góc vuông)
Mà \(IC=ID=r\Rightarrow ICOD\) là hình vuông
\(S_{IEF}+S_{IEO}+S_{IFO}=\dfrac{1}{2}\left(IG.EF+IC.EO+ID.FO\right)\)
\(=\dfrac{1}{2}r\left(EF+EO+FO\right)\) (do \(IG=IC=ID=r\))
\(=S_{OEF}=\dfrac{1}{2}OM.EF=\dfrac{1}{2}R.EF\)
\(\Rightarrow\dfrac{r}{R}=\dfrac{EF}{EF+OE+OF}>\dfrac{EF}{EF+EF+EF}=\dfrac{1}{3}\)
(do tam giác OEF vuông nên \(OE< EF;OF< EF\))