Cho hpt (a+1)x-ay=5 và x+ay=a^2 +4a. Tìm a nguyên để hpt có nghiệm (x:y) sao cho x;y là số nguyên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|\dfrac{4}{3}x-\dfrac{1}{4}\right|>=0\forall x\)
=>\(A=\left|\dfrac{4}{3}x-\dfrac{1}{4}\right|-\dfrac{2}{11}>=-\dfrac{2}{11}\forall x\)
Dấu '=' xảy ra khi \(\dfrac{4}{3}x-\dfrac{1}{4}=0\)
=>\(\dfrac{4}{3}x=\dfrac{1}{4}\)
=>\(x=\dfrac{1}{4}:\dfrac{4}{3}=\dfrac{3}{16}\)

a: 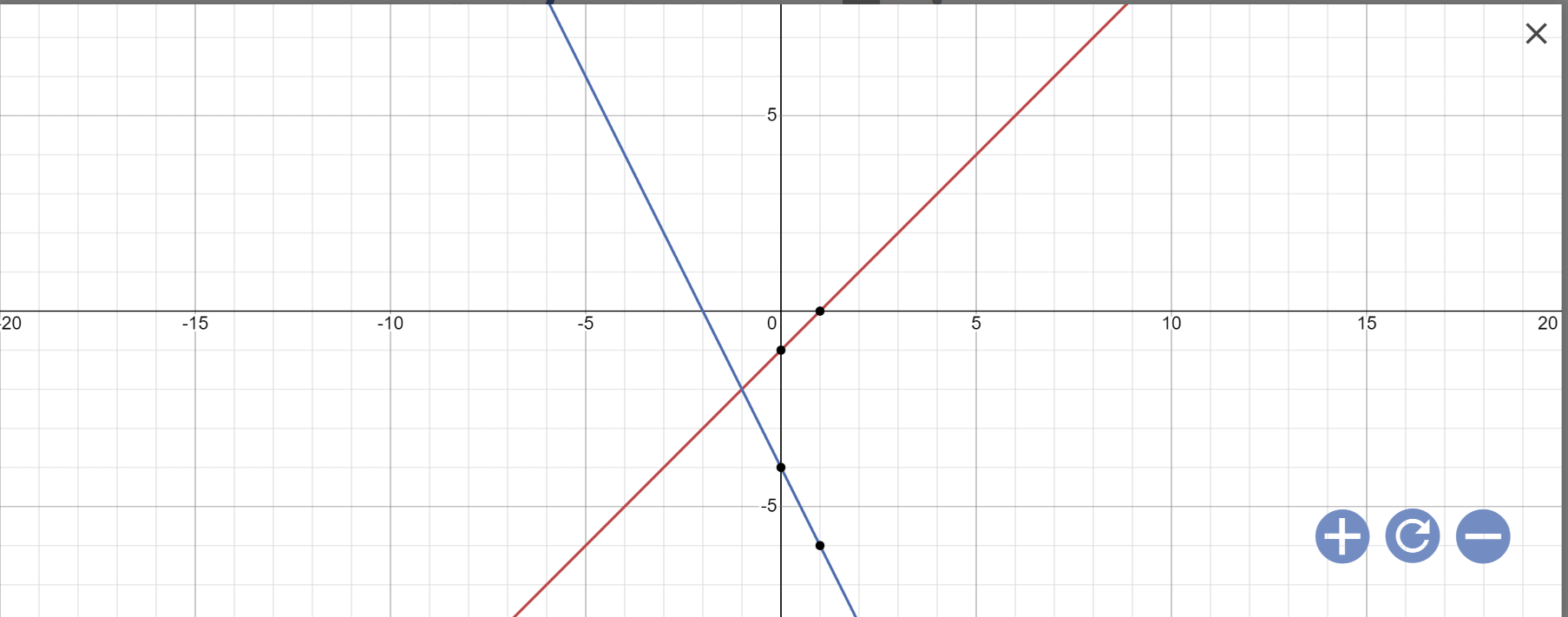
b: Phương trình hoành độ giao điểm là:
-2x-4=x-1
=>-2x-x=-1+4
=>-3x=3
=>x=-1
Thay x=-1 vào y=x-1, ta được:
y=-1-1=-2
Vậy: Tọa độ giao điểm là A(-1;-2)

\(\left|6x+22\right|>=0\forall x;\left(y-21\right)^2>=0\forall y\)
Do đó: \(\left|6x+22\right|+\left(y-21\right)^2>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}6x+22=0\\y-21=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{11}{3}\\y=21\end{matrix}\right.\)

45:(3x-6)=5
=>3x-6=45:5=9
=>3x=9+6=15
=>\(x=\dfrac{15}{3}=5\)

\(\left(x^2+1\right)\left(x-1\right)=0\)
mà \(x^2+1>=1>0\forall x\)
nên x-1=0
=>x=1

a: \(\left|-\dfrac{1}{3}\right|-\left(-\dfrac{6}{7}\right)^0+\left(\dfrac{1}{2}\right)^2:2\)
\(=\dfrac{1}{3}-1+\dfrac{1}{4}:2=-\dfrac{2}{3}+\dfrac{1}{8}=\dfrac{-16}{24}+\dfrac{3}{24}=-\dfrac{13}{24}\)
b: \(\left(\dfrac{2}{3}\right)^3+\sqrt{\dfrac{49}{81}}-\left|-\dfrac{7}{3}\right|:3\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{3}\cdot\dfrac{1}{3}\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{9}=\dfrac{8}{27}\)
c: \(\sqrt{\dfrac{25}{49}}+\left(5555\right)^0+\left|-\dfrac{2}{7}\right|\)
\(=\dfrac{5}{7}+1+\dfrac{2}{7}\)
=1+1=2

`180 = 2.2. 3.3 . 5`
`2024 = 2.2.2 . 11 . 23`
`1500 = 2.2.3.5.5.5`
`400 = 2.2.2.2.5.5`
`504 = 2.2.2.3.3.7`
`890 = 2.5.89`

d: \(\left|-5-\sqrt{2}\right|=5+\sqrt{2}\)
c: \(\left|4+\sqrt{3}\right|=4+\sqrt{3}\)
d: \(\left|-\dfrac{4}{15}\right|=\dfrac{4}{15}\)
a: \(\left|3,02\right|=3,02\)


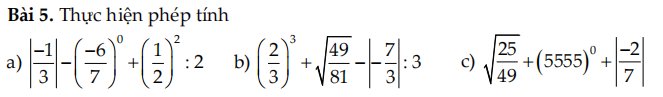
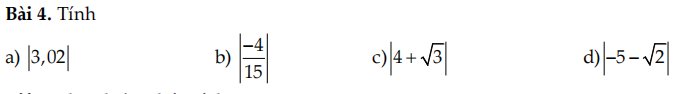
Để hệ có nghiệm duy nhất thì \(\dfrac{a+1}{1}\ne\dfrac{-a}{a}=-1\)
=>\(a+1\ne-1\)
=>\(a\ne-2\)
\(\left\{{}\begin{matrix}\left(a+1\right)x-ay=5\\x+ay=a^2+4a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)x-ay+x+ay=5+a^2+4a\\x+ay=a^2+4a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(a+2\right)=a^2+4a+5\\ay=a^2+4a-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\ay=a^2+4a-\dfrac{a^2+4a+5}{a+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\ay=\dfrac{\left(a+2\right)\left(a^2+4a\right)-a^2-4a-5}{a+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\y=\dfrac{a^3+4a^2+2a^2+8a-a^2-4a-5}{a\left(a+2\right)}=\dfrac{a^3+5a^2+4a-5}{a\left(a+2\right)}\end{matrix}\right.\)
Để x,y nguyên thì \(\left\{{}\begin{matrix}a^2+4a+5⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a^2+4a+4+1⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a+2\in\left\{1;-1\right\}\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a\in\left\{-1;-3\right\}\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\Leftrightarrow a=-1\)