
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
\(A=3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\\ 3A=3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\\ 3A+A=\left(3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\right)+\left(3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\right)\\ 4A=3^{101}+1\\ A=\dfrac{3^{101}+1}{4}\)

Bài 13:
Chu vi của hình tam giác đó là:
\(6,8+10,5+7,9=25,2\left(cm\right)\)
ĐS: ...
Bài 14:
Chiều dài của sân là:
\(86,7+21,6=108,3\left(m\right)\)
Chu vi của sân là:
\(2\times\left(86,7+108,3\right)=390\left(m\right)\)
ĐS: ...


Gọi số học sinh đi tham quan là \(a\)
Điều kiện: \(a\inℕ^∗;700\le a\le1200\)
Ta có:
+) Nếu xếp 30 em hay 45 em vào 1 xe thì đều thiếu 5 em
⇒\(a\) chia \(30\) hay \(45\) thiếu \(5\)
\(\Rightarrow a+5⋮30;45\)
\(\Rightarrow a+5\in BC\left(30;45\right)=\left\{0,90,180,270,360,450,540,630,720,810,900,990,1080,1170,1260,...\right\}\)
Mà \(700\le a\le1200\) nên \(705\le a+5\le1205\) suy ra:
\(a\in\left\{720,810,900,990,1080,1170\right\}\)
+) Nếu xếp 43 em vào một xe thì vừa đủ
\(\Rightarrow a⋮43\)
Do đó: \(a=1075\) (thỏa mãn điều kiện)
Vậy...
Gọi tổng số h/s là A
A:30 thiếu 5 , chia 45 cũng thiếu 5 ≠Ta có :
A+5 ∈ BCNN(45,30)700≤A≤1200
30=2.3.5
45=2.3.3.5=2.32.5
BCNN(30,45)=2.95=90
BC(30,45)={0,90,180,270,360,450,540,630,720,810,900,990,1080,1170} mà 700≤A≤1200 nên loại các số 0,90,180,270,360,450,540,630.
Nếu A là 1 trong các số trên thì phải trừ đi 5 , A ∈={715,805,895,985,1075,1165}
Vì A⋮43 nên A sẽ bằng 1075 , vậy chuyến đi đó có 1075 h/s lớp 6
Đáp số 1075 h/s

Số huy chương Đồng đoàn thể thao Việt Nam nhận được là:
288 - 183 = 105 (huy chương)
ĐS: ...

Ta có BĐT Bunhiacopxki:
\(\left(1\cdot\sqrt{a}+1\cdot\sqrt{b}\right)^2\le\left(1^2+1^2\right)\left(a+b\right)\Leftrightarrow\sqrt{a}+\sqrt{b}\le\sqrt{2\left(a+b\right)}\) (*)
Dấu "=" xảy ra khi: \(\dfrac{\sqrt{a}}{1}=\dfrac{\sqrt{b}}{1}\Leftrightarrow a=b\)
a) \(2\le x\le4\)
Áp dụng bđt (*) ta có:
\(A=\sqrt{x-2}+\sqrt{4-x}\le\sqrt{2\left(x-2+4-x\right)}=2\)
Dấu "=" xảy ra khi: \(x-2=4-x\Leftrightarrow x=3\) (tm)
b) \(-2\le x\le6\)
Áp dụng bđt (*) ta có:
\(B=\sqrt{6-x}+\sqrt{x+2}\le\sqrt{2\left(6-x+x+2\right)}=4\)
Dấu "=" xảy ra khi: \(6-x=x+2\Leftrightarrow x=2\left(tm\right)\)
c) \(0\le x\le2\)
\(C=\sqrt{x}+\sqrt{2-x}\le\sqrt{2\left(x+2-x\right)}=2\)
Dấu "=" xảy ra khi: \(x=2-x\Leftrightarrow x=1\left(tm\right)\)

\(1)\left(\dfrac{1}{5}\right)^5\cdot5^5\\ =\left(\dfrac{1}{5}\cdot5\right)^5\\ =1^5\\ =1\\ 2)\left(\dfrac{2}{5}\right)^9\cdot5^9\\ =\left(\dfrac{2}{5}\cdot5\right)^9\\ =2^9\\ 3)\left(\dfrac{4}{9}\right)^3\cdot3^3\\ =\left(\dfrac{4}{9}\cdot3\right)^3\\ =\left(\dfrac{4}{3}\right)^3\\ 4)\left(\dfrac{3}{7}\right)^2\cdot\left(-7\right)^4\\ =\left(\dfrac{3}{7}\right)^2\cdot\left[\left(-7\right)^2\right]^2\\ =\left(\dfrac{3}{7}\right)^2\cdot49^2\\ =\left(\dfrac{3}{7}\cdot49\right)^2\\ =\left(3\cdot7\right)^2\\ =21^2\\ 5)\left(-11\right)^{12}\cdot\left(\dfrac{4}{11}\right)^6\\ =\left[\left(-11\right)^2\right]^6\cdot\left(\dfrac{4}{11}\right)^6\\ =121^6\cdot\left(\dfrac{4}{11}\right)^6\\ =\left(121\cdot\dfrac{4}{11}\right)^6\\ =\left(4\cdot11\right)^6\\ =44^6\\ 6)\left(-6\right)^8\cdot\left(\dfrac{5}{6}\right)^7\\ =\left(-6\right)\cdot\left(-6\right)^7\cdot\left(\dfrac{5}{6}\right)^7\\ =\left(-6\right)\cdot\left(-6\cdot\dfrac{5}{6}\right)^7\\ =\left(-6\right)\cdot\left(-5\right)^7\)



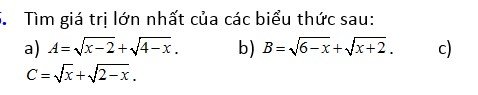

1) Đặt: \(\dfrac{1}{x}=u;\dfrac{1}{y-2}=v\)
\(=>\left\{{}\begin{matrix}2u+3v=4\\4u-v=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4u+6v=8\\4u-v=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}7v=7\\4u-v=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v=1\\u=\dfrac{1}{2}\end{matrix}\right.\)
\(=>\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{2}\\\dfrac{1}{y-2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
2) Đặt: \(\dfrac{1}{x+1}=u;\dfrac{1}{y}=v\)
\(=>\left\{{}\begin{matrix}2u+3v=-1\\2u+5v=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2u+3v=-1\\2v=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2u=-1\\v=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u=-\dfrac{1}{2}\\v=0\end{matrix}\right.\\ =>\left\{{}\begin{matrix}\dfrac{1}{x+1}=-\dfrac{1}{2}\\\dfrac{1}{y}=0\end{matrix}\right.=>x,y\in\varnothing\)
3) Đặt: \(\dfrac{1}{x}=u;\dfrac{1}{y-2}=v\)
\(=>\left\{{}\begin{matrix}u-v=-1\\4u+3v=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4u-4v=-4\\4u+3v=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}v=\dfrac{9}{7}\\u=\dfrac{2}{7}\end{matrix}\right.\\ =>\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{9}{7}\\\dfrac{1}{y-2}=\dfrac{2}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{9}\\y-2=\dfrac{7}{2}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{9}\\y=\dfrac{7}{2}+2=\dfrac{11}{2}\end{matrix}\right.\)