Với các số thực a và b thỏa mãn a2 + b2 = 2, tìm giá trị nhỏ nhất của biểu thức P = 3(a + b) + ab.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\dfrac{a+2}{a-2}\left(ĐK:a>0;a\ne\left\{1;4\right\}\right)\\ =\left(\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\right).\dfrac{a-2}{a+2}\\ =\left(\dfrac{a+\sqrt{a}+1}{\sqrt{a}}-\dfrac{a-\sqrt{a}+1}{\sqrt{a}}\right).\dfrac{a-2}{a+2}\\ =\dfrac{2\sqrt{a}}{\sqrt{a}}.\dfrac{a-2}{a+2}=\dfrac{2\left(a-2\right)}{a+2}\)

\(\dfrac{3\sqrt{x}+8}{\sqrt{x}+2}-\dfrac{10}{3}>0\)
\(ĐK:x\ge0\)
\(\Leftrightarrow\dfrac{9\sqrt{x}+24-10\sqrt{x}-20}{3\left(\sqrt{x}+2\right)}>0\)
\(\Leftrightarrow\dfrac{-\sqrt{x}+4}{3\left(\sqrt{x}+2\right)}>0\)
\(\Leftrightarrow-\sqrt{x}+4>0\) ( vì \(3\left(\sqrt{x}+2\right)>0\) )
\(\Leftrightarrow\sqrt{x}-4< 0\)
\(\Leftrightarrow\sqrt{x}< 4\)
\(\Leftrightarrow x< 16\)
Vậy \(S=\left\{x|0\le x< 16\right\}\)
\(ĐK:x>=0\)
\(\dfrac{3\sqrt{x}+8}{\sqrt{x}+2}-\dfrac{10}{3}>0\\ < =>\dfrac{3\left(3\sqrt{x}+8\right)-10\left(\sqrt{x}+2\right)}{3\left(\sqrt{x}+2\right)}>0\\ < =>\dfrac{9\sqrt{x}+24-10\sqrt{x}-20}{3\left(\sqrt{x}+2\right)}>0\\ < =>\dfrac{-\sqrt{x}+4}{3\left(\sqrt{x}+2\right)}>0\)
Vì : \(3\left(\sqrt{x}+2\right)>0\forall x>=0\)
\(=>-\sqrt{x}+4>0\\ < =>-\sqrt{x}>-4\\< => \sqrt{x}< 4\\< =>0\le x< 16\)

`@`Xét tam giác ABC vuông A, đường cao AH:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
\(CH+BC-BH=10-3,6=6,4\left(cm\right)\)
\(AH=\sqrt{BH.CH}=\sqrt{3,6.6,4}=4,8\left(cm\right)\)
`@`Xét tam giác AHB vuông H, đường cao HM:
\(\dfrac{1}{HM^2}=\dfrac{1}{BH^2}+\dfrac{1}{AH^2}\)
\(\Leftrightarrow\dfrac{1}{HM^2}=\dfrac{1}{3,6^2}+\dfrac{1}{4,8^2}\)
\(\Leftrightarrow HM=2,88\left(cm\right)\)
\(BM=\sqrt{BH^2-HM^2}=\sqrt{3,6^2-2,88^2}=2,16\left(cm\right)\)
`@`Xét tam giác AHC vuông H, đường cao HN:
\(\dfrac{1}{HN^2}=\dfrac{1}{HC^2}+\dfrac{1}{AH^2}\)
\(\Leftrightarrow\dfrac{1}{HN^2}=\dfrac{1}{6,4^2}+\dfrac{1}{4,8^2}\)
\(\Leftrightarrow HN=3,84\left(cm\right)\)
\(NC=\sqrt{HC^2-HN^2}=\sqrt{6,4^2-3,84^2}=5,12\left(cm\right)\)
`@`Ta có: \(\left\{{}\begin{matrix}\widehat{B}+\widehat{MHB}=90^o\\\widehat{C}+\widehat{NHC}=90^o\\\widehat{B}+\widehat{C}=90^o\end{matrix}\right.\) \(\rightarrow\widehat{MHN}=90^o\)
Ta có:
\(S_{BHM}=\dfrac{1}{2}.MB.MH=\dfrac{1}{2}.2,16.2,88=3,1104\left(cm^2\right)\)
\(S_{NHC}=\dfrac{1}{2}.NH.NC=\dfrac{1}{2}.3,84.5,12=9,8304\left(cm^2\right)\)
\(S_{MHN}=\dfrac{1}{2}.MH.NH=\dfrac{1}{2}.2,88.3,84=5,5296\left(cm^2\right)\)
\(S_{BCNM}=S_{BHM}+S_{NHC}+S_{MHN}\)
\(=3,1104+9,8304+5,5296\)
\(=18,4704\left(cm^2\right)\)

\(\left\{{}\begin{matrix}a+b\le10\\b\le7\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}b\le7\\a\le3\end{matrix}\right.\) ⇔ P ≤ 32 + 72 = 58
P(max)= 58 ⇔ a =3; b = 7
a ≥ 0; b ≥ 0 ⇔P = a2 + b2≥ 0 + 0 = 0 ⇔ P(min) = 0 ⇔ a=b=0

4x2y + 8xy2 + 5x + 10y = 1
<=> (4xy + 5)(x + 2y) = 1
<=> (4xy + x2 + 4y2)(x + 2y) = 1
<=> (x + 2y)3 = 1
<=> x + 2y = 1
<=> x = 1 - 2y
Khi đó x2 + 4y2 = 5
<=> (1 - 2y)2 + 4y2 = 5
<=> 8y2 - 4y - 4 = 0
<=> 2y2 - y - 1 = 0
<=> (y - 1)(2y + 1) = 0
<=> \(\left[{}\begin{matrix}y=1\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Khi y = 1 => x = 1 - 2y = -1
Khi y = \(-\dfrac{1}{2}\Rightarrow x=1-2y=2\)
(x;y) = (-1;1) ; (2;-1/2)

\(P=\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x+1}{\sqrt{x}}\left(ĐK:x>0;x\ne1\right)\\ =\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}+\dfrac{x+1}{\sqrt{x}}\\ =\dfrac{x+2\sqrt{x}+1}{\sqrt{x}}=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)
\(P=\dfrac{9}{2}< =>\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}=\dfrac{9}{2}\\ < =>2\left(x+2\sqrt{x}+1\right)=9\sqrt{x}\\ < =>2x-5\sqrt{x}+2=0\\ < =>\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\\ =>\left[{}\begin{matrix}\sqrt{x}-2=0\\2\sqrt{x}-1=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=4\left(TM\right)\\x=\dfrac{1}{4}\left(TM\right)\end{matrix}\right.\)

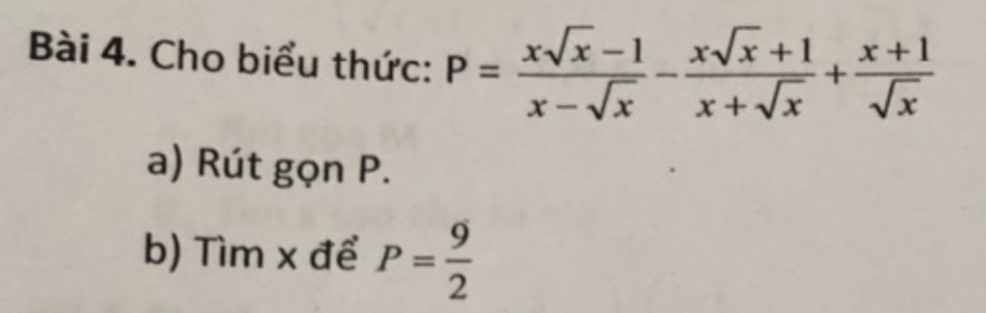
\(a^2+b^2=2\)
\(\Leftrightarrow\left(a+b\right)^2-2ab=2\)
\(\Leftrightarrow2ab=\left(a+b\right)^2-2\)
Theo đề: \(P=3\left(a+b\right)+ab\)
\(\Leftrightarrow2P=6\left(a+b\right)+2ab\)
\(=6\left(a+b\right)+\left(a+b\right)^2-2\)
\(=\left(a+b\right)^2+2.3\left(a+b\right)+9-9-2\)
\(=\left[\left(a+b\right)+3\right]^2-11\)
\(P=\dfrac{1}{1}\left(a+b+3\right)^2-\dfrac{11}{2}\)
Ta có: \(\left(a+b+3\right)^2\ge0\forall a,b\in R\)
\(\Leftrightarrow\dfrac{1}{2}\left(a+b+3\right)^2-\dfrac{11}{2}\ge\dfrac{-11}{2}\forall a,b\in R\)
=> Giá trị nhỏ nhất \(P=-\dfrac{11}{2}\)