chảnh quá đề đâu hả

đề

 Ta có \(\left(x+10\right)^4+\left(x-3\right)^4=\left[\left(x+10\right)^2\right]^2+\left[\left(3-x\right)^2\right]^2\)

\(\ge\dfrac{\left[\left(x+10\right)^2+\left(3-x\right)^2\right]^2}{2}\) \(\ge\dfrac{\left[\dfrac{\left(x+10+3-x\right)^2}{2}\right]^2}{2}\) \(=\dfrac{\left(\dfrac{13^2}{2}\right)^2}{2}\)\(=\dfrac{28561}{8}\) (áp dụng 2 lần bất đẳng thức \(a^2+b^2\ge\dfrac{\left(a+b\right)^2}{2}\))

 Suy ra \(P\le2000-\dfrac{28561}{8}=-\dfrac{12561}{8}\).

 Dấu "=" xảy ra \(\Leftrightarrow x+10=3-x\Leftrightarrow x=-\dfrac{7}{2}\)

 Vậy \(maxP=-\dfrac{12561}{8}\), max xảy ra khi \(x=-\dfrac{7}{2}\)

\(A=-x^2-4x\)

\(\Rightarrow A=-x^2-4x-4+4\)

\(\Rightarrow A=-\left(x^2+4x+4\right)+4\)

\(\Rightarrow A=-\left(x+2\right)^2+4\)

mà \(-\left(x+2\right)^2\le0,\forall x\)

\(\Rightarrow A=-\left(x+2\right)^2+4\le0+4=4\)

Vậy GTLN của A là 4

\(B=-9x^2+24x-18\)

\(\Rightarrow B=-9x^2+24x-16+16-18\)

\(\Rightarrow B=-\left(9x^2-24x+16\right)+16-18\)

\(\Rightarrow B=-\left(3x-4\right)^2-2\)

mà \(-\left(3x-4\right)^2\le0,\forall x\)

\(\Rightarrow B=-\left(3x-4\right)^2-2\le0-2=-2\)

Vậy GTLN của B là -2

   3a\(x\)² + 3b\(x\)² + a\(x\) + b\(x\) + 5a + 5b 

= (3a\(x^2\) + 3b\(x^2\)) + (a\(x\) + b\(x\)) + (5a + 5b)

= 3\(x^2\)(a + b) + \(x\)(a +b) + 5(a + b)

= (a + b)( 3\(x^2\) + \(x\) + 5)

= (a + b)(3\(x^2\) + \(x\) + 5)²

Yêu cầu đề bài của bạn

A = - \(x^2\) - 4\(x\)

A = -(\(x^2\) + 4\(x\) + 4) + 4

A = -(\(x\) + 2)² + 4 

Vì (\(x\) + 2)² ≥ 0 ⇒ -(\(x\) + 2)² ≤ 0 ⇒ - (\(x\) + 2)² + 4  ≤ 4

⇒ A_max = 4 ⇔ \(x\) + 2 = 0 ⇔ \(x\) = -2

Kết luận giá trị lớn nhất của A là 4 xảy ra khi \(x\) = -2

B = - 9\(x^2\) + 24\(x\) - 18

B = - (9\(x^2\) - 24\(x\) + 16) - 2

B = -(3\(x\) - 4)² - 2 

(3\(x\) - 4)² ≥ 0 ⇒ -(3\(x\) - 4)² ≤ 0 ⇒ -(3\(x\) - 4)² - 2 ≤ -2 

B_max = -2 ⇔ 3\(x\)   - 4 = 0 ⇔ \(x\) = \(\dfrac{4}{3}\) 

Kết luận giá trị lớn nhất của B là: -2 xảy ra khi \(x\) = \(\dfrac{4}{3}\) 

A = 2\(x\) - \(x^2\) - 4

A = -(\(x^2\) - 2\(x\) + 1)  - 3

A = - (\(x-1\))² - 3

Vì (\(x-1\))² ≥ 0 ⇒ -(\(x\) - 1)² ≤ 0  ⇒ -( \(x\) - 1)² - 3 ≤ - 3

A_max = -3  ⇔ \(x\) - 1 = 0 ⇔ \(x\) = 1

Vậy giá trị lớn nhất của biểu thức là 0 xảy ra khi \(x\) = 1

B = - \(x^2\) - 4\(x\) 

B = -( \(x^2\) + 4\(x\) + 4) + 4

B = -(\(x\) + 2)² + 4

Vì (\(x\) + 2)² ≥ 0 ⇒ - (\(x\) + 2)² ≤ 0 ⇒ -(\(x+2\))²  + 4  ≤ 0 

B_max = 4 ⇔ \(x+2=0\Rightarrow x=-2\)

Kết luận giá trị lớn nhất của biểu thức là 4 xảy ra khi \(x\) = - 2

\(\left(25x^2-2\right)=\left(5x-\sqrt[]{2}\right)\left(5x+\sqrt[]{2}\right)\)

đề là j v bn ơi

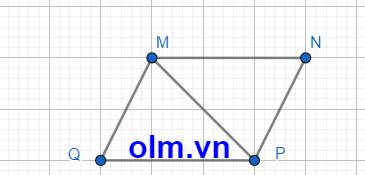
Xét \(\Delta\)MPQ và \(\Delta\)PMN có: 

MP chung

\(\widehat{QPM}\) = \(\widehat{PMN}\)  (2 góc so le trong)

\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)

\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)

\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)

b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:

         MP chung

         MN = PQ 

  \(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)

⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)

\(\Rightarrow\) MQ = NP (đpcm)

⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\) 

   Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:

   QM // NP (đpcm)

`x^2+x+1=x^2+x+1/4+3/4=(x+1/2)^2 +3/4`

Vì `(x+1/2)^2 >= 0` với mọi `x`

  `=>(x+1/2)^2 +3/4 >= 3/4` với mọi `x`

 `=>` Biểu thức Min `=3/4<=>x=-1/2`

_____________

`(x-3)(x+5)+4=x^2+2x-11=x^2+2x+1-12=(x+1)^2-12`

  Vì `(x+1)^2 >= 0` với mọi `x`

    `=>(x+1)^2-12 >= -12` với mọi `x`

 `=>` Biểu thức Min `=-1/2<=>x=-1`