An và Bình có tổng cộng 180 viên bi. Sau khi An cho Bình 47 viên bi, thì số bi của Bình gấp đôi số bi của An. Hỏi ban đầu mỗi bạn có bao nhiêu viên bi ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi d=UCLN(a;b)
=> Tồn tại 2 số nguyên m;n sao cho
a=md và b=nd
ta có
a+b=md+nd=d(m+n)=p\(\Rightarrow p⋮d\) mà p là số nguyên tố nên d=1
=> a và b nguyên tố cùng nhau

TH1: Nếu con gà chạy sang chuồng 2 là một con gà mái thì lúc này chuồng 2 có 7 con gà trống và 4 con gà mái \(\Rightarrow\) P(gà trống) \(=\dfrac{7}{11}\)
TH2: Nếu con gà chạy sang chuồng 2 là một con gà trống thì lúc này chuồng 2 có 8 con gà trống và 3 con gà mái \(\Rightarrow\) P(gà trống) \(=\dfrac{8}{11}\)
Bởi chuồng 1 có số lượng gà trống và gà mái bằng nhau nên xác suất để 1 con gà trống hay 1 con gà mái chạy từ chuồng 1 sang chuồng 2 là như nhau.
\(\Rightarrow\) P(gà trống) \(=\dfrac{\dfrac{7}{11}+\dfrac{8}{11}}{2}=\dfrac{15}{22}\)
2) Bạn bổ sung thêm đề bài nhé.

\(D=\dfrac{6-1}{1.6}+\dfrac{11-6}{6x11}+\dfrac{16-11}{11x16}+...+\dfrac{56-51}{51.56}=\)
\(=1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{51}-\dfrac{1}{56}=1-\dfrac{1}{56}=\dfrac{55}{56}\)

gọi d là UC(2n+1; 3n+1) nên
\(2n+1⋮d\Rightarrow3\left(2n+1\right)=6n+3⋮d\)
\(3n+1⋮d\Rightarrow2\left(3n+1\right)=6n+2⋮d\)
\(\Rightarrow6n+3-\left(6n+2\right)=1⋮d\Rightarrow d=1\)
=> 2n+1 và 3n+1 nguyên tố cùng nhau
Gọi d là ước chung lớn nhất của 2n + 1 và 3n + 1.
Ta có:
![[Năm 2021] Đề thi Học kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều](https://vietjack.com/de-thi/images/de-thi-hoc-ki-1-toan-lop-6-co-dap-an-canh-dieu-71573.png)
![[Năm 2021] Đề thi Học kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều](https://vietjack.com/de-thi/images/de-thi-hoc-ki-1-toan-lop-6-co-dap-an-canh-dieu-71574.png)
Do đó d = ±1
Do đó: ƯCLN (2n + 1; 3n + 1) = 1
Vậy hai số 2n + 1 và 3n + 1 nguyên tố cùng nhau (với n không thuộc N)

\(a,-\dfrac{5}{7}+1+\dfrac{30}{-7}\le x\le-\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{5}{6}\\ \dfrac{-5+1.7-30}{7}\le x\le\dfrac{-1+1.2+5}{6}\\ -\dfrac{28}{7}\le x\le\dfrac{6}{6}\\ -4\le x\le1\\ Vậy:x\in\left\{-4;-3;-2;-1;0;1\right\}\)
\(b,\dfrac{-8}{13}+\dfrac{7}{17}+\dfrac{21}{13}\le x\le-\dfrac{9}{14}+3+\dfrac{5}{-14}\\ \left(\dfrac{21}{13}-\dfrac{8}{13}\right)+\dfrac{7}{17}\le x\le\left(-\dfrac{9}{14}-\dfrac{5}{14}\right)+3\\ 1+\dfrac{7}{17}\le x\le-1+3\\ 1\dfrac{7}{17}\le x\le2\\ Vậy:x=2\)

1 hàng cầm số bông hoa là:
5x2=10 (bông hoa)
Đội hoạt náo viên cầm tất cả số bông hoa là:
10x8=80 (bông hoa)
Đáp số:80 bông hoa
Đội náo viên cầm tất cả số bông tua là:
8x5x2=20 (bông tua)
Đ/S:...

S=1.2+2.3+3.4+...+68.69
⇒ 3S= 1.2.3+2.3.3+3.4.3+...+68.69.3
3S=1.2.3+2.3.(4-1)+3.4.(5-2)+...+68.69.(70-67)
3S=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+68.69.70-67.68.69
3S=68.69.70
⇒ S=\(\dfrac{68.69.70}{3}\)=328440

Ta có: \(\overline{abc}\) \(\times\) \(\overline{cb}\) = \(\overline{abcd}\)
\(\overline{abc}\) \(\times\) \(\overline{cb}\) = \(\overline{abc}\) \(\times\) 10 + d
d = \(\overline{abc}\) \(\times\) \(\overline{cb}\) - \(\overline{abc}\) \(\times\) 10
d = \(\overline{abc}\) \(\times\) (\(\overline{cb}\) - 10); \(\overline{abc}\) ≥ 100;
vậy d = 0 nên \(\overline{cb}\) - 10 = 0
\(\overline{cb}\) = 10
c = 1; b = 0 Vì a;b;c là 3 số liên tiếp nên a = c + 1 = 2
Thay a = 2; b = 0; c = 1 vào \(\overline{abc5}\) ta được: \(\overline{abc5}\) = 2015
Đáp số:..

a; A = \(\dfrac{3n+1}{2n+3}\) (đk n \(\in\) Z)
A \(\in\) N ⇒ 3n + 1 ⋮ 2n + 3
2.(3n + 1) ⋮ 2n + 3
6n + 2 ⋮ 2n + 3
3(2n + 3) - 7 ⋮ 2n + 3
7 ⋮ 2n + 3
7 = 7 ⇒ Ư(7) = {-7; -1; 1; 7}
Lập bảng ta có:
| 2n + 3 | -7 | -1 | 1 | 7 |
| n | -5 | -2 | -1 | 2 |
| A = \(\dfrac{3n+1}{2n+3}\) | 2 | 5 | -2 (loại) | 1 |
Theo bảng trên ta có: n \(\in\) {-5; -2; 2}
B = \(\dfrac{3n-5}{2n-1}\) (đk n \(\in\) Z)
B \(\in\) N ⇔ 3n - 5 ⋮ 2n - 1
2.(3n - 5) ⋮ 2n - 1
6n - 10 ⋮ 2n - 1
6n - 3 - 7 ⋮ 2n - 1
3.(2n - 1) - 7 ⋮ 2n - 1
7 ⋮ 2n - 1
7 = 7 ⇒ Ư(7) = {-7; - 1; 1; 7}
Lập bảng ta có:
| 2n - 1 | -7 | -1 | 1 | 7 |
| n | -3 | 0 | 1 | 4 |
| B = \(\dfrac{3n-5}{2n-1}\) | 2 | 5 | -2 (loại) | 1 |
Theo bảng trên ta có:
n \(\in\) {-3; 0; 4}
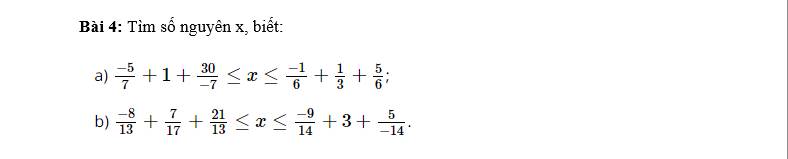
Tổng số phần bằng nhau: 1+2=3(phần)
Khi An cho Bình 47 viên bi, số bi của Bình lúc này là: 180 : 3 x 2 = 120 (viên)
Số bi ban đầu của Bình: 120 - 47 = 73 (viên)
Số bi ban đầu của An: 180 - 73 = 107 (viên)
Đ.số: An có 107 viên bi, Bình có 73 viên bi