S=5+5^2+5^3+5^4+...+5^2019 chứng minh S chia hết cho 21
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAPE vuông tại P và ΔAPH vuông tại P có
AP chung
PE=PH
Do đó: ΔAPE=ΔAPH
Xét ΔAQH vuông tại Q và ΔAQF vuông tại Q có
AQ chung
QH=QF
Do đó; ΔAQH=ΔAQF
b: ΔAPE=ΔAPH
=>\(\widehat{PAE}=\widehat{PAH}\)
=>AP là phân giác của góc HAE
ΔAQH=ΔAQF
=>\(\widehat{QAH}=\widehat{QAF}\)
=>AQ là phân giác của góc HAF
\(\widehat{EAF}=\widehat{EAH}+\widehat{FAH}\)
\(=2\widehat{QAH}+2\cdot\widehat{PAH}=2\cdot\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot\widehat{QAP}=180^0\)
=>E,A,F thẳng hàng


Bài 1
Tổng số phần bằng nhau:
4 + 5 = 9 (phần)
Số bao gạo ban đầu xe thứ nhất chở:
153 : 9 × 4 + 10 = 78 (bao)
Số bao gạo ban đầu xe thứ hai chở:
153 - 78 = 75 (bao)
Bài 2
Tổng số tuổi của ông và cháu sau hai năm nữa:
74 + 2 × 2 = 78 (tuổi)
Tổng số phần bằng nhau:
1 + 12 = 13 (phần)
Tuổi ông hiện nay:
78 : 13 × 12 - 2 = 70 (tuổi)
Tuổi cháu hiện nay:
74 - 70 = 4 (tuổi)

Bài 6: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{142^0}{2}=71^0\)
Ta có: \(\widehat{xOz}+\widehat{x'Oz}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oz}+71^0=180^0\)
=>\(\widehat{x'Oz}=109^0\)
Bài 7:
Ta có: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}=90^0\)
Ot là phân giác của góc xOz
=>\(\widehat{zOt}=\dfrac{\widehat{xOz}}{2}=\dfrac{90^0}{2}=45^0\)
Ov là phân giác của góc yOz
=>\(\widehat{vOz}=\dfrac{90^0}{2}=45^0\)
\(\widehat{vOt}=\widehat{zOv}+\widehat{zOt}=45^0+45^0=90^0\)

a) \(\dfrac{12}{5}>\dfrac{10}{5}=2=\dfrac{4}{2}>\dfrac{3}{2}\) (Số 2 làm trung gian)
Hay \(\dfrac{12}{5}>\dfrac{3}{2}\)
b) Ta có:
`2023 < 2024 =>` \(\dfrac{2023}{2024}< 1\)
`2026 > 2025 =>` \(\dfrac{2026}{2025}>1\)
=> \(\dfrac{2023}{2024}< 1< \dfrac{2026}{2025}\) (1 làm trung gian)
Hay \(\dfrac{2023}{2024}< \dfrac{2026}{2025}\)
a: \(\dfrac{12}{5}=2,4;\dfrac{3}{2}=1,5\)
mà 2,4>1,5
nên \(\dfrac{12}{5}>\dfrac{3}{2}\)
b: \(\dfrac{2023}{2024}< \dfrac{2024}{2024}=1;\dfrac{2026}{2025}>\dfrac{2025}{2025}=1\)
Do đó: \(\dfrac{2023}{2024}< \dfrac{2026}{2025}\)

Sửa đề: \(\dfrac{0,375-0,3+\dfrac{3}{11}+\dfrac{3}{12}}{-0,625+0,5-\dfrac{5}{11}-\dfrac{5}{12}}+\dfrac{1,5+1-0,75}{2,5+\dfrac{5}{3}-1,25}\)
\(=\dfrac{\dfrac{3}{8}-\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}}{-\dfrac{5}{8}+\dfrac{5}{10}-\dfrac{5}{11}-\dfrac{5}{12}}+\dfrac{\dfrac{3}{2}+\dfrac{3}{3}-\dfrac{3}{4}}{\dfrac{5}{2}+\dfrac{5}{3}-\dfrac{5}{4}}\)
\(=\dfrac{3\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}{-5\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}+\dfrac{3\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}{5\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}\)
\(=\dfrac{3}{-5}+\dfrac{3}{5}=0\)

780-(x-45):2=120
=>(x-45):2=780-120=660
=>\(x-45=660\times2=1320\)
=>x=1320+45=1365

b: \(\dfrac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}\cdot\dfrac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}=8^x\)
=>\(8^x=\dfrac{4\cdot4^5}{3\cdot3^5}\cdot\dfrac{6\cdot6^5}{2\cdot2^5}\)
=>\(8^x=\dfrac{4^6}{2^6}\cdot\dfrac{6^6}{3^6}=2^6\cdot2^6=2^{12}=\left(2^3\right)^4=8^4\)
=>x=4

1: \(5^{x+4}-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(5^{x+3}\cdot5-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(2\cdot5^{x+3}=2\cdot5^{11}\)
=>x+3=11
=>x=8
2: \(\dfrac{1}{2}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\cdot\left(\dfrac{1}{2}+4\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=2^6\)
=>x=6
3: \(9^{2x+1}=27^3\)
=>\(3^{4x+2}=3^9\)
=>4x+2=9
=>4x=7
=>\(x=\dfrac{7}{4}\)
4: \(2^{-1}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\left(4+\dfrac{1}{2}\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=9\cdot2^5:\dfrac{9}{2}=2^6\)
=>x=6
5: \(\left(2x-1\right)^3=\dfrac{8}{27}\)
=>\(\left(2x-1\right)^3=\left(\dfrac{2}{3}\right)^3\)
=>\(2x-1=\dfrac{2}{3}\)
=>\(2x=\dfrac{2}{3}+1=\dfrac{5}{3}\)
=>\(x=\dfrac{5}{3}:2=\dfrac{5}{6}\)


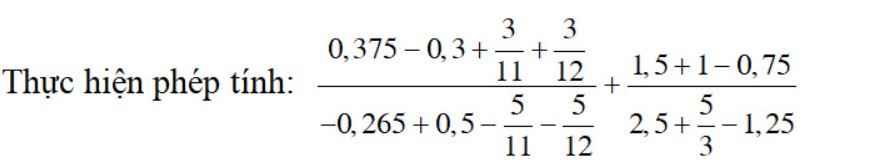
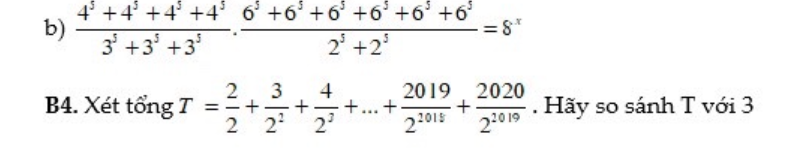
sửa đề chia hết 31 nhé
\(S=5+5^2+5^3+...+5^{2019}=5\left(1+5+5^2+5^3\right)+...+5^{2016}\left(1+5+5^2+5^3\right)\)
\(=31\left(5+...+5^{2016}\right)⋮31\)
Vậy ta có đpcm