Bài 11. Cho tam giác ABC vuông ở A, có C = 30°, đường cao AH. Trên đoạn HC lấy điểm D saocho HD = HB.Từ C kẻ CE vuông góc với đường thẳng AD(E thuộc AD)
1. Chứng minh rằng: ABH = ADH.
2. Chứng minh rằng: ABD đều.
3. Chứng minh rằng: AH = EC.
4. Gọi giao điểm của AH và CE là I. Chứng minh rằng ID vuông góc AC.
5. Chứng minh rằng: HE vuông góc IC.


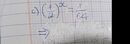
còn cái nịt