3/Ta có  |x+2| và |2y+3| luôn lớn hơn hoặc bằng 0

Để  |x+2|+|2y+3|=0

=>x+2=0 và 2y+3=0

=>x=-2 và y=-3/2

1) Nếu x  < 1,5 

=> |2x - 3| = -2x + 3

|2 - x| = 2 - x

Khi đó |2x - 3| - x = |2 - x| (1)

<=> -2x + 3 - x = 2 - x

<=> -2x = -1

<=> x = 0,5 (tm)

Khi \(1,5\le x\le2\)

=> |2x - 3| = 2x - 3

|2 - x| = 2 - x

Khi đó |2x - 3| - x = |2 - x|

<=> 2x  -3 - x = 2 - x

<=> 2x = 5

<=> x = 2,5 (loại) 

Khi x > 2

=> |2x - 3| = 2x - 3

|2 - x| = x - 2

Khi đó (1) <=> 2x - 3 - x = x - 2

<=> 0x = 1 

=> x \(\in\varnothing\)

Vậy x = 0,5 là giá  trị cần tìm 

a ) Gọi I là giao điểm của BD và AE.

Xét tam giác ABI và tam giác EBI có:

          AB=EB (tam giác ABD=tam giác EBD)

          Góc ABI=góc EBI (đường phân giác BD)

          BI là cạnh chung.

=> tam giác ABI=tam giác EBI (c.g.c)

=> AI=EI => I là trung điểm của AE. (1)

=> Góc BIA=góc BIE

Mà góc BIA+góc BIE=180 độ (hai góc kề bù)

=> góc BIA=góc BIE=90 độ.

=> BI vuông góc với AE (2).

Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AE

/x-2/-/2x-3/-x=-2

/x-2/-/2x-3/=-2+x

/x-2/-/2x-3/=x-2

Nếu /x-2/=x-2 thì /2x-3/=0 =>2x-3=0 =>x=1,5

Nếu /x-2/=-(x-2) thì 

-(x-2)-/2x-3/=x-2

-x+2-/2x-3/=x-2

Thực hiện quy tắc chuyển vế ta đc

-/2x-3/=2x-4

=>/2x-3/=-(2x-4)

Nếu 2x-3=-(2x-4)

2x-3=-2x+4

4x=7

x=7/4

Nếu 2x-3=2x-4

2x-2x=-4+3

0=-1 ( vô lí)

Vậy x có thể 7/4

Câu a

Câu 1:Góc nào vậy ???

Câu 2: C

Câu 3: A

Trả lời:

= 100

~HT~

Đáp án:

Math so Easy

7x2+6+80

=14+6+80

=20+80

=100

\(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2005}}\)

\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2004}}\)

\(A=1-\frac{1}{2^{2005}}\)

a) \(\left|4-x\right|+2x=3\)

<=> \(\left|4-x\right|=3-2x\)

<=> \(\orbr{\begin{cases}4-x=3-2x\left(x\le4\right)\\x-4=3-2x\left(x>4\right)\end{cases}}\)

<=> \(\orbr{\begin{cases}x=-1\left(tm\right)\\3x=7\end{cases}}\)

<=> \(\orbr{\begin{cases}x=-1\\x=\frac{7}{3}\left(ktm\right)\end{cases}}\)

Vậy x = -1

b) \(\left|x-7\right|+2x+5=6\)

<=> \(\left|x-7\right|=1-2x\)

<=> \(\orbr{\begin{cases}x-7=1-2x\left(đk:x\ge7\right)\\x-7=2x-1\left(đk:x< 7\right)\end{cases}}\)

<=> \(\orbr{\begin{cases}3x=8\\x=-6\left(tm\right)\end{cases}}\)

<=> \(\orbr{\begin{cases}x=\frac{8}{3}\left(ktm\right)\\x=-6\left(tm\right)\end{cases}}\)

Vậy x = -6

c) \(3x-\left|2x+1\right|=2\)

<=> \(\left|2x+1\right|=3x-2\)

<=> \(\orbr{\begin{cases}2x+1=3x-2\left(đk:x\ge-\frac{1}{2}\right)\\2x+1=2-3x\left(đk:x< -\frac{1}{2}\right)\end{cases}}\)

<=> \(\orbr{\begin{cases}x=3\left(tm\right)\\5x=1\end{cases}}\)

<=> \(\orbr{\begin{cases}x=3\\x=\frac{1}{5}\left(ktm\right)\end{cases}}\)

Vậy x = 3

d) \(\left|x+2\right|-x=2\)

<=> \(\left|x+2\right|=x+2\)

<=> \(\orbr{\begin{cases}x+2=x+2\left(đk:x\ge-2\right)\\x+2=-x-2\left(x< -2\right)\end{cases}}\)

<=> \(\orbr{\begin{cases}0x=0\\2x=-4\end{cases}}\)

<=> 0x = 0 (luôn đúng) và x = -2 (ktm)

Vậy x \(\ge\)-2

e) \(\left|x-3\right|=21\)

<=> \(\orbr{\begin{cases}x-3=21\\3-x=21\end{cases}}\)

<=> \(\orbr{\begin{cases}x=24\\x=-18\end{cases}}\)

Vậy x = 24 hoặc x = -18

f) \(\left|2x+3\right|-\left|x-3\right|=0\)

<=> \(\left|2x+3\right|=\left|x-3\right|\)

<=> \(\orbr{\begin{cases}2x+3=x-3\\2x+3=3-x\end{cases}}\)

<=> \(\orbr{\begin{cases}x=-6\\3x=0\end{cases}}\)

<=> \(\orbr{\begin{cases}x=-6\\x=0\end{cases}}\)

Vậy x thuộc {-6; 0}

g) Ta có: \(\left|x+\frac{1}{8}\right|\ge0\forall x\)

          \(\left|x+\frac{2}{8}\right|\ge0\forall x\)

    \(\left|x+\frac{5}{8}\right|\ge0\forall x\)

=> VT = \(\left|x+\frac{1}{8}\right|+\left|x+\frac{2}{8}\right|+\left|x+\frac{5}{8}\right|\ge0\forall x\)

=> VP \(\ge0\) => \(4x\ge0\) => \(x\ge0\)

Do đó: \(x+\frac{1}{8}+x+\frac{2}{8}+x+\frac{5}{8}=4x\)

<=> \(3x+1=4x\) <=> \(x=1\left(tm\right)\)

Vậy x = 1

h) \(\left|x-2\right|-\left|2x+3\right|-x=-2\)

<=> \(\left|x-2\right|-\left|2x+3\right|=x-2\)(*)

Lập bảng xét dấu: 

x                     -3/2              2

x - 2        2 - x    |        2 - x    0        x - 2

2x + 3  -2x - 3   0      2x + 3  |          2x + 3

Xét x < -3/2 => pt (*) trở thành: 2 - x + 2x + 3 = x - 2

<=> x + 5 = x - 2 <=> 0x = -7 (vô lí)

Xét -3/2 \(\le\) x < 2 => pt (*) trở thành: 2 - x - 2x - 3 = x - 2

<=> 4x = 1 <=> x = 1/4 ((tm)

Xét x \(\ge\) 2 => pt (*) trở thành x - 2 - 2x - 3 = x - 2

<=> 2x = -3 <=>  x = -3/2 (ktm)

Vậy x = 1/4

i) |2x - 3| - x = |2 - x|

<=> |2x - 3| - |2 - x| = x (*)

Lập bảng xét dấu

x                    3/2               2

2x - 3   3 - 2x   0     2x - 3   |  2x - 3

2 - x     2 - x     |       2 - x    0   x - 2

Xét x < 3/2 => pt (*) trở thành: 3 - 2x - 2 + x =  x

<=> 2x = 1 <=> x = 1//2 ((tm)
Xét \(\frac{3}{2}\le x< 2\)=> pt (*) trở thành: 2x - 3 - 2 + x = x

<=> 2x = 5 <=> x = 5/2 (ktm)

Xét x \(\ge\)2 ==> pt (*) trở thành: 2x - 3 - x + 2 = x

<=> 0x = -5 (vô lí)

Vậy x = 1/2

k) 2|x - 3| - |4x - 1| = 0

<=> 2|x - 3| = |4x - 1|

<=> \(\orbr{\begin{cases}2\left(x-3\right)=4x-1\\2\left(x-3\right)=1-4x\end{cases}}\)

<=> \(\orbr{\begin{cases}2x-6=4x-1\\2x-6=1-4x\end{cases}}\)

<=> \(\orbr{\begin{cases}2x=-5\\6x=7\end{cases}}\)

<=> \(\orbr{\begin{cases}x=-\frac{5}{2}\\x=\frac{7}{6}\end{cases}}\) Vậy ...

Tìm x

\(\left|x-4\right|+2x=5\)

\(\left|x-4\right|=5-2x\)

Ta có: \(\left|x-4\right|\ge0\forall x\)

\(\Rightarrow5-2x\ge0\)

\(\Rightarrow2x\le5\)

\(\Rightarrow x\le2,5\)

\(\left|x-4\right|=5-2x\Rightarrow\orbr{\begin{cases}x-4=5-2x\\x-4=2x-5\end{cases}}\Rightarrow\orbr{\begin{cases}x+2x=5+4\\x-2x=-1\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)

Vì \(x\le2,5\) nên x = 1

Vậy x = 1.

\(|x-4|+2x=5\)

\(|x-4|=5-2x\)

\(\Leftrightarrow\orbr{\begin{cases}x-4=5-2x\\x-4=2x-5\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}3x=9\\-1x=-1\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)

Bạn tham khảo !

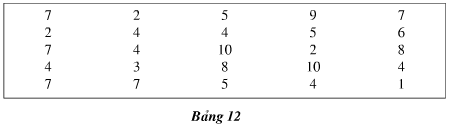
a) Dấu hiệu: tuổi nghề của công nhân trong một phân xưởng. Số các giá trị: 25.

b) Bảng tần số về tuổi nghề

Nhận xét:

Số các giá trị của dấu hiệu: 25
Số các giá trị khác nhau: 10, giá trị lớn nhất là 10, giá trị nhỏ nhất là 1.
Giá trị có tần số lớn nhất là 4.
Các giá trị thuộc vào khoảng chủ yếu từ 4 đến 7 năm.