

 giup minh voi
giup minh voi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{2a+b+c+d}{a}=\frac{a+2b+c+d}{b}=\frac{a+b+2c+d}{c}=\frac{a+b+c+d+2d}{d}=\)
\(=\frac{2a+b+c+d+a+2b+c+d+a+b+2c+d+a+b+c+2d}{a+b+c+d}=\)
\(=\frac{5\left(a+b+c+d\right)}{a+b+c+d}=5\)
Từ \(\frac{a+b+2c+d}{c}=\frac{a+b+c+2d}{d}=\frac{2\left(a+b\right)+3\left(c+d\right)}{c+d}=\)
\(=\frac{2\left(a+b\right)}{c+d}+3=5\Rightarrow\frac{a+b}{c+d}=1\)
C/m tương tự có \(\frac{b+c}{d+a}=\frac{c+d}{a+b}=\frac{d+a}{b+c}=1\)
\(\Rightarrow\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{b+c}=4\)

\(b^2=a.c\)\(=>\frac{a}{b}=\frac{b}{c}\)
Đặt : \(\frac{a}{b}=\frac{b}{c}=k\)
Ta có : \(a=b.k\)
\(b=c.k\)
\(=>\)\(\frac{a}{c}=\frac{b.k}{c}=\frac{c.k+k}{c}=k^2\left(1\right)\)
\(\left(\frac{a+2012b}{b+2012c}\right)^2=\left(\frac{bk+2012b}{ck+2012c}\right)^2=\left(\frac{b\left(k+2012\right)}{c\left(k+2012\right)}\right)^2=\left(\frac{b}{c}\right)^2=k^2\left(2\right)\)
Từ (1) và (2) \(=>\frac{a}{c}=\left(\frac{a+2012b}{b+2012c}\right)^2\left(đpcm\right)\)
Hok tốt~

Ta có : \(\frac{a}{b}=\frac{c}{d}=k\)
\(=>a=bk\) và \(b=dk\)
Lại có:
\(\frac{ac}{bd}\)\(=\frac{bk.dk}{bd}=\frac{bd.k^2}{bd}\)\(=k^2\)
\(\frac{a^2+c^{ }^2}{b^2+d^2}\)\(=\frac{\left(bk\right)^2.\left(dk\right)^2}{b^2+d^2}\)\(\frac{b^2.k^2+d^2.k^2}{b^2+d^2}=\frac{k^2\left(b^2+d^2\right)}{b^2+d^2}\)\(=k^2\)
\(=>\frac{ac}{bd}=\frac{b^2+c^2}{b^2+d^2}\)\(\left(đpcm\right)\)
Hok tốt~

\(\left(3n+5\right)⋮\left(n^2+1\right)\Rightarrow3n\left(3n+5\right)=9n^2+15n⋮\left(n^2+1\right)\)
\(9n^2+15n=9n^2+9+15n+25-34=9\left(n^2+1\right)+5\left(3n+5\right)-34\)
Suy ra \(34⋮\left(n^2+1\right)\)
mà \(n\)là số tự nhiên nên \(n^2+1\inƯ\left(34\right)=\left\{1,2,17,34\right\}\)
suy ra \(n\in\left\{0,1,4\right\}\).
Thử lại đều thỏa mãn.

a^2 = b^2 ; c^2 = d^2
=> a = b ; c = d
=> ab = a^2 = b^2 ; cd = c^2 = d^2
=> đpcm

( 6x /7 + 1 ) : ( -9 ) = -2/27
=> ( 6x /7 + 1 ) = -2/27 * ( -9 )
=> 6x /7 + 1 = 2/3
=> 6x /7 = 2/3 - 3/3
=> 6x /7 = -1/3
=> 6x = -7/3
=> x = -7/3 : 6
=> x = -7/18


Gọi cân nặng của Bình, Tâm, An lần lượt là \(a,b,c\left(kg\right);a,b,c>0\).
Vì số cân nặng ba bạn lần lượt tỉ lệ với \(9,10,11\)nên
\(\frac{a}{9}=\frac{b}{10}=\frac{c}{11}\).
Vì Tâm nặng hơn Bình \(10kg\)nên \(c-a=10\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{9}=\frac{b}{10}=\frac{c}{11}=\frac{c-a}{11-9}=\frac{10}{2}=5\)
\(\Leftrightarrow\hept{\begin{cases}a=5.9=45\\b=5.10=50\\c=5.11=55\end{cases}}\)(tm)

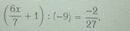
 lm hộ mik b2->
lm hộ mik b2->