Xét tam giác ABC vuông tại A có đường cao AH
a) Tính số đo góc HBA
b) Kẻ HD vuông góc AC tại D. Chứng minh: AD.AC = HB.HC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 36:
a.
Nếu $a,b>0$ thì:
\(A=\frac{\sqrt{a}-\sqrt{b}}{\sqrt{b}}.\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}}:\frac{a^2-b^2}{ab}\\ =\frac{a-b}{\sqrt{ab}}.\frac{ab}{(a-b)(a+b)}=\frac{\sqrt{ab}}{a+b}\)
Nếu $a,b<0$ thì:
\(A=\frac{\sqrt{-a}-\sqrt{-b}}{\sqrt{-b}}.\frac{\sqrt{-a}+\sqrt{-b}}{\sqrt{-a}}:\frac{a^2-b^2}{ab}\\ =\frac{(-a)-(-b)}{\sqrt{ab}}.\frac{ab}{(a-b)(a+b)}=\frac{\sqrt{ab}}{-(a+b)}\)
Vậy không có đáp án đúng.
b.
$b=1$ thì $b>0, a>0$.
Khi đó: $A=\frac{\sqrt{ab}}{a+b}=2$
$\Leftrightarrow \frac{\sqrt{a}}{a+1}=2$
$\Leftrightarrow \sqrt{a}=2a+2$
$\Leftrightarrow 2a-\sqrt{a}+2=0$
$\Leftrightarrow (\sqrt{a}-0,5)^2+a+1,75=0$
$\Leftrightarrow (\sqrt{a}-0,5)^2+a=-1,75<0$ (vô lý với mọi $a>0$)
Đáp án D.

\(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2\sqrt{2}}{\sqrt{2}+1}-\left(3+\sqrt{3}-2\sqrt{2}\right)\\ =\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{2\sqrt{2}\left(\sqrt{2}-1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}-3-\sqrt{3}+2\sqrt{2}\\ =\sqrt{3}+2+\dfrac{4-2\sqrt{2}}{2-1}-3-\sqrt{3}+2\sqrt{2}\\ =-1+2\sqrt{2}+\dfrac{4-2\sqrt{2}}{1}\\ =-1+2\sqrt{2}+4-2\sqrt{2}\\ =3\)

1) \(\dfrac{\sqrt[]{6}+\sqrt[]{14}}{2\sqrt[]{3}+\sqrt[]{28}}=\dfrac{\sqrt[]{2}\left(\sqrt[]{3}+\sqrt[]{7}\right)}{2\left(\sqrt[]{3}+\sqrt[]{7}\right)}=\dfrac{\sqrt[]{2}}{2}\)
2) \(\dfrac{\sqrt[]{5}-\sqrt[]{10}}{\sqrt[]{3}-\sqrt[]{6}}=\dfrac{\sqrt[]{5}\left(1-\sqrt[]{2}\right)}{\sqrt[]{3}\left(1-\sqrt[]{2}\right)}=\sqrt[]{\dfrac{5}{3}}\)
3) \(...=\dfrac{4\sqrt[]{2}-2\sqrt[]{3}}{3\sqrt[]{2}-4\sqrt[]{3}}-\dfrac{\sqrt[]{5}+\sqrt[]{27}}{\sqrt[]{6}\left(\sqrt[]{5}+\sqrt[]{27}\right)}\)
\(=\dfrac{2\left(2\sqrt[]{2}-\sqrt[]{3}\right)}{3\sqrt[]{2}-4\sqrt[]{3}}-\dfrac{1}{\sqrt[]{6}}\)
\(=\dfrac{2\sqrt[]{6}\left(2\sqrt[]{2}-\sqrt[]{3}\right)-\left(3\sqrt[]{2}-4\sqrt[]{3}\right)}{\sqrt[]{6}\left(3\sqrt[]{2}-4\sqrt[]{3}\right)}\)
\(=\dfrac{8\sqrt[]{3}-6\sqrt[]{2}-3\sqrt[]{2}+4\sqrt[]{3}}{6\sqrt[]{3}-12\sqrt[]{3}}\)
\(=\dfrac{12\sqrt[]{3}-9\sqrt[]{2}}{-6\sqrt[]{3}}=-2+\sqrt[]{\dfrac{3}{2}}\)
Bài 4 bạn tự làm nhé

\(17-\dfrac{12}{\sqrt[]{2}}=17-6\sqrt[]{2}=18-6\sqrt[]{2}+1-2\)
\(=\left(\sqrt[]{18}-1\right)^2-2=\left(3\sqrt[]{2}-1\right)^2-2\)

Bài 1 :
\(...\Rightarrow A=\dfrac{\sqrt[]{x}\left(\sqrt[]{x}+2\right)+\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}-2\right)}{\left(\sqrt[]{x}-2\right)\left(\sqrt[]{x}+2\right)}-\dfrac{\sqrt[]{x}-10}{x-4}\)
\(\Rightarrow A=\dfrac{x+2\sqrt[]{x}+x-3\sqrt[]{x}+2}{x-4}-\dfrac{\sqrt[]{x}-10}{x-4}\)
\(\Rightarrow A=\dfrac{2x-\sqrt[]{x}+2-\sqrt[]{x}+10}{x-4}\)
\(\Rightarrow A=\dfrac{2x-2\sqrt[]{x}+12}{x-4}=\dfrac{2\left(x-\sqrt[]{x}+6\right)}{x-4}\)

Ta có:
\(P=\left(2+\sqrt{2}\right)^7+\left(2-\sqrt{2}\right)^7\)
\(P=2^7+7.2^6\sqrt{2}+21.2^5\left(\sqrt{2}\right)^2+...+7.2\left(\sqrt{2}\right)^6+\left(\sqrt{2}\right)^7\)\(+2^7-7.2^6\sqrt{2}+21.2^5\left(\sqrt{2}\right)^2-...+7.2\left(\sqrt{2}\right)^6-\left(\sqrt{2}\right)^7\)
\(P=2.2^7+2.21.2^5.\left(\sqrt{2}\right)^2+2.35.2^3.\left(\sqrt{2}\right)^4+2.7.2.\left(\sqrt{2}\right)^6\)
\(P=2^8+21.2^7+35.2^6+7.2^5\)
\(P=5408\)
\(\Rightarrow\left(2+\sqrt{2}\right)^7=5408-\left(2-\sqrt{2}\right)^7\)
Do \(0< \left(2-\sqrt{2}\right)^7< 1\) nên suy ra \(5047< \left(2+\sqrt{2}\right)^7< 5048\)
Vậy số nguyên lớn nhất không vượt quá \(\left(2+\sqrt{2}\right)^7\) là 5047.
(Sau này ta kí hiệu như thế này cho gọn.)

ĐKXĐ : \(x\inℝ\)
Ta có : x2 + 4x + 7 = (x + 4)\(\sqrt{x^2+7}\)
\(\Leftrightarrow x^2+7+4x=x\sqrt{x^2+7}+4\sqrt{x^2+7}\) (*)
Đặt \(\sqrt{x^2+7}=a>0\)
Có (*) \(\Leftrightarrow a^2+4x=ax+4a\)
\(\Leftrightarrow\left(a-x\right).\left(a-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=x\\a=4\end{matrix}\right.\)
Với a = x \(\Leftrightarrow\sqrt{x^2+7}=x\Leftrightarrow\left\{{}\begin{matrix}x^2+7=x^2\\x>0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
Với a = 4 \(\Leftrightarrow\sqrt{x^2+7}=4\Leftrightarrow x^2+7=16\Leftrightarrow x=\pm3\)
Thử lại thấy thỏa mãn
Tập nghiệm \(S=\left\{\pm3\right\}\)
\(x^2+4x+7=\left(x+4\right)\sqrt[]{x^2+7}\)
\(\Leftrightarrow x^2+7+4x=\left(x+4\right)\sqrt[]{x^2+7}\left(1\right)\)
Đặt \(t=\sqrt[]{x^2+7}\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2+4x=\left(x+4\right).t\)
\(\Leftrightarrow t^2-\left(x+4\right).t+4x=0\)
\(\Leftrightarrow t^2-tx-4.t+4x=0\)
\(\Leftrightarrow t\left(t-x\right)-4\left(t-x\right)=0\)
\(\Leftrightarrow\left(t-x\right)\left(t-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t-x=0\\t-4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}t=x\\t=4\end{matrix}\right.\)
- Với \(t=x\Leftrightarrow\sqrt[]{x^2+7}=x\Leftrightarrow x^2+7=x^2\Leftrightarrow0.x^7=7\left(loại\right)\)
- Với \(t=4\Leftrightarrow\sqrt[]{x^2+7}=4\Leftrightarrow x^2+7=16\Leftrightarrow x^2=9\Leftrightarrow x=\pm3\)
Vậy nghiệm phương trình là \(\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
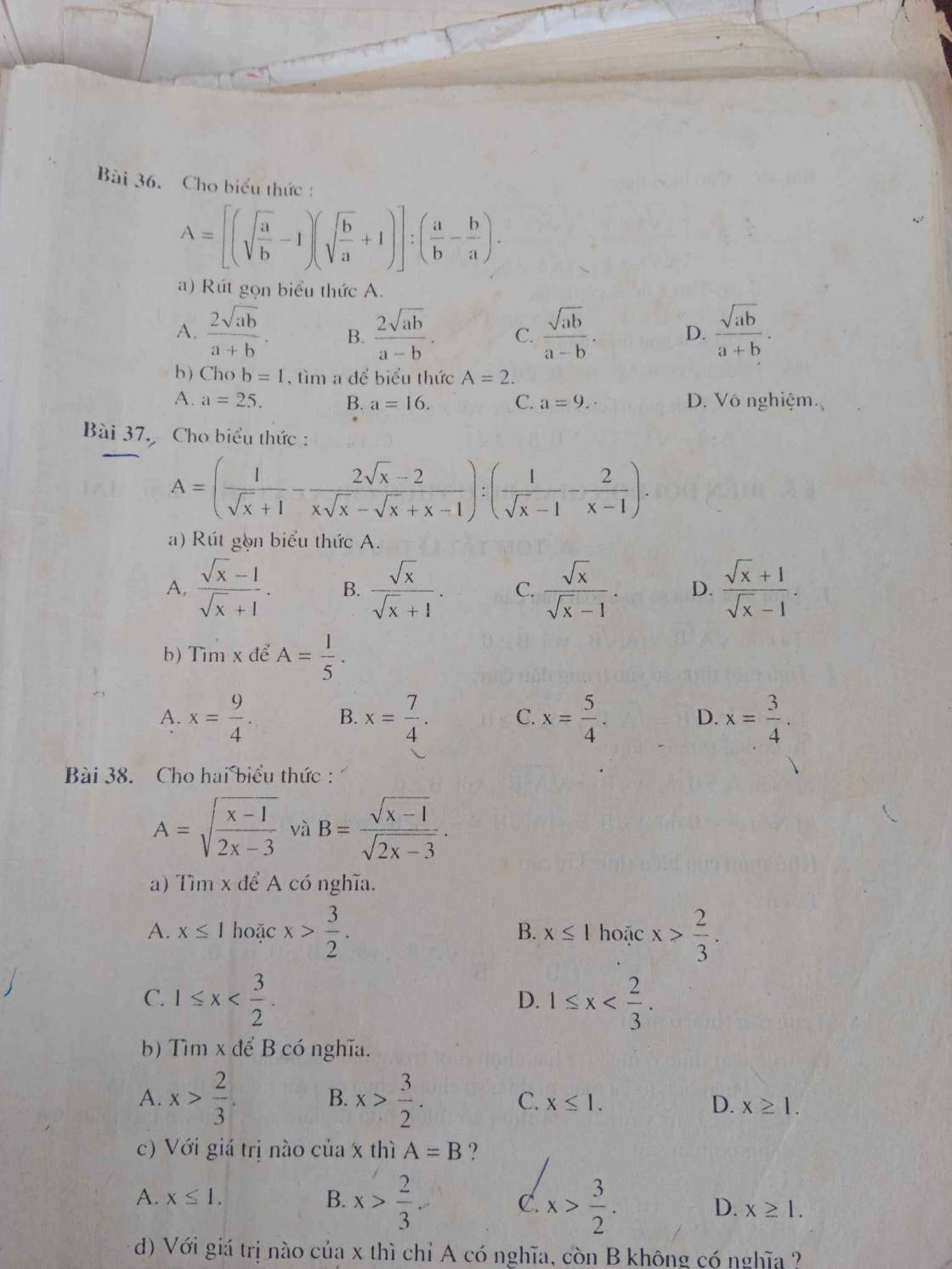
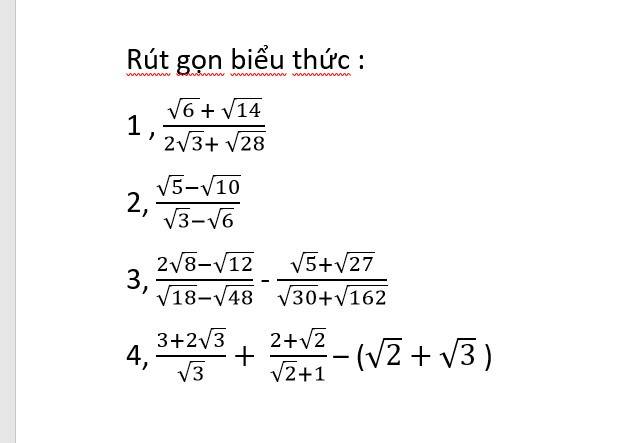

`a,` Ta có `ΔABC` vuông tại `A,`
`=>` `HBA` là góc vuông, có số đo là `90^o`
`b,` Ta có `ΔABC` vuông tại `A`
`=>` `AH` là đường cao của `ΔABC`
Theo định lý Euclid, trong một tam giác vuông, đường cao chia tam giác thành hai tam giác nhỏ có tỉ lệ bằng độ dài các cạnh gần góc vuông.
Vậy ta có: `(AD)/(AB)` `=` `(HD)/(HC)`
Vì `ΔABC` vuông tại `A`
`=> AB` `= AC`
`=>` `(AD)/(AC)` `=` `(HD)/(HC)`
Nhân cả hai vế của phương trình trên với `AC,` ta có:
`AD .` `(AC)/(AC)` `= HD .` `(HC)/(HC)`
`AD =` `HD.``HC`
`=>` `AD.AC` `=` `HB.HC.`
a) 90o,
b).............................. =) AD.AC = HB.HC