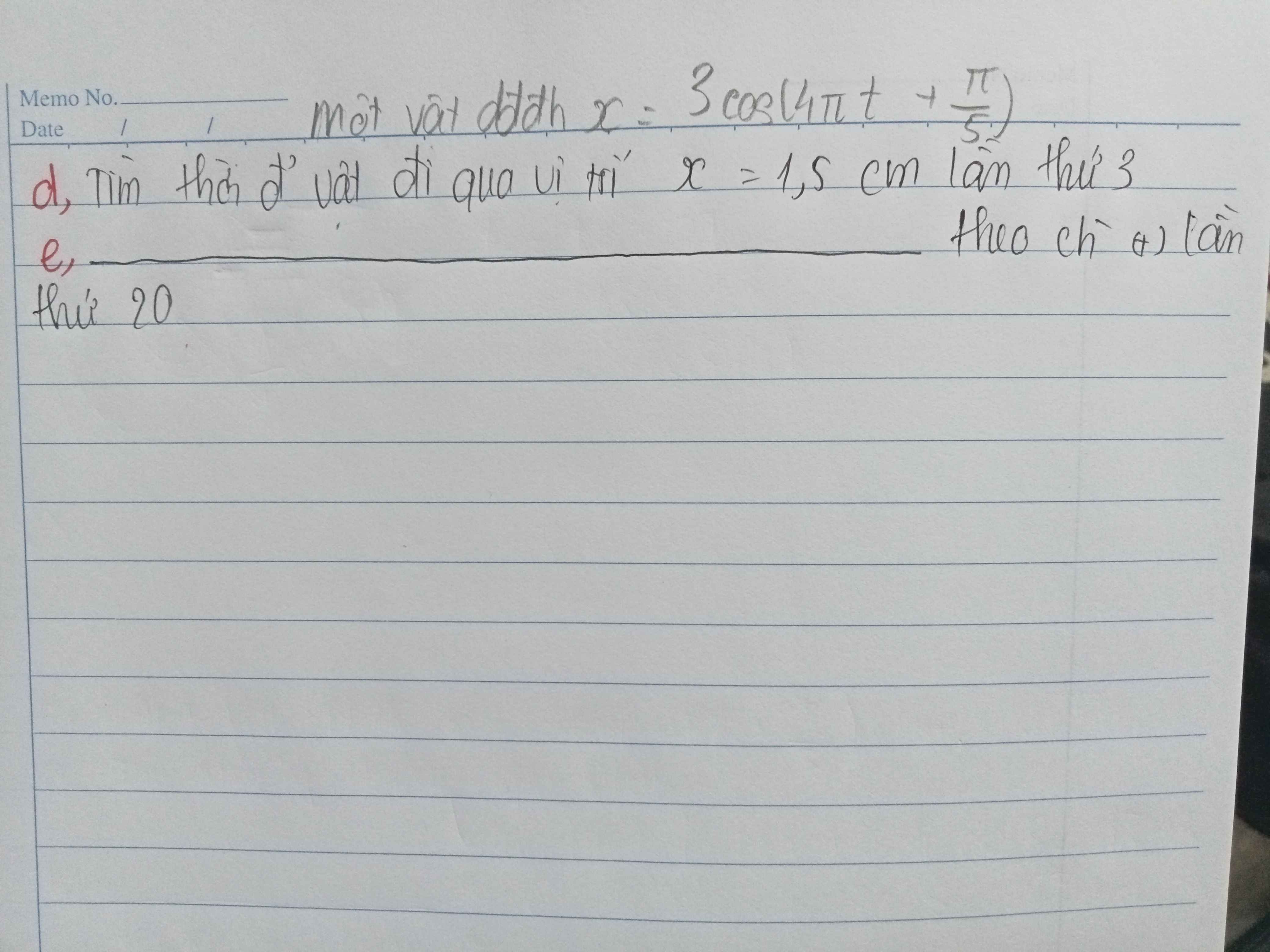\(\left\{{}\begin{matrix}V+v=18\\V-v=12\end{matrix}\right.\Leftrightarrow\left(V,v\right)=\left(15,3\right)\)

 Đặt \(AB=s\left(km\right)\) thì \(t_{xuôi}=\dfrac{s}{18}\left(h\right),t_{ngược}=\dfrac{s}{12}\left(h\right)\) 

 Theo đề bài, ta có: \(\dfrac{s}{18}+\dfrac{s}{12}=2,5\Leftrightarrow s=18\left(km\right)\)

 Nếu vận tốc dòng nước là \(v\left(km/h\right)\) và vận tốc thực của thuyền là \(V\left(km/h\right)\) thì:

 \(\left\{{}\begin{matrix}V+v=18\\V-v=12\end{matrix}\right.\Leftrightarrow\left(V,v\right)=\left(15,3\right)\). Vậy \(v_{nước}=3km/h\)

 Có \(t_{xuôi}=\dfrac{s}{18}=\dfrac{18}{18}=1\left(h\right)\), \(t_{ngược}=\dfrac{s}{12}=\dfrac{18}{12}=1,5\left(h\right)\)

Gọi thời gian chuyển động của vật là \(t\)

Khi đó \(s_t=v_0t+\dfrac{1}{2}at^2=0.t+\dfrac{1}{2}.2t^2=t^2\)

\(s_{t-1}=v_0\left(t-1\right)+\dfrac{1}{2}a\left(t-1\right)^2=\left(t-1\right)^2\)

Trong giây cuối vật đi được 25m

\(\Leftrightarrow t^2-\left(t-1\right)^2=25\)

\(\Leftrightarrow2t-1=25\)

\(\Leftrightarrow t=13\)

Vậy thời gian vật chuyển động là 13 giây.

?

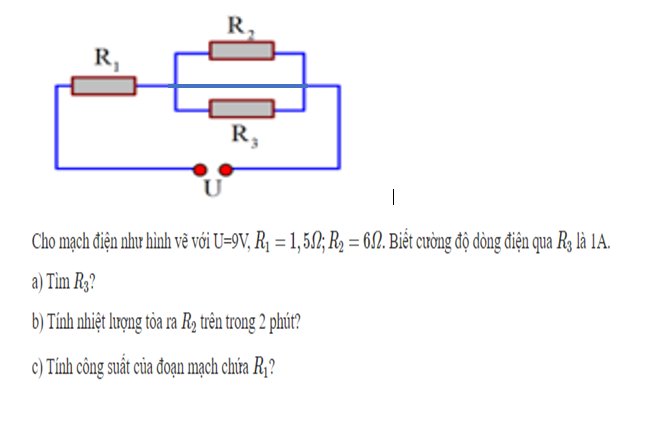
Đoạn mạch AB gồm R₁ mắc nối tiếp với (R₂//R₃) nên I = I₁ = I₂₃.

Điện trở tương đương của toàn mạch là

\(R_{tđ}=R_1+R_{23}=R+\dfrac{3}{2}R=1,5R\)

Ta có công suất tiêu thụ trên R₁ là 16 W, suy ra:

\(P_1=I^2_1R_1=I^2R=16\) W.

Công suất tiêu thụ trên toàn mạch là

\(P=I^2R_{tđ}=I^2.1,5R=1,5.16=24\) W.

Dao động điều hòa có mặt khắp nơi trong cuộc sống hàng ngày và trong nhiều lĩnh vực kỹ thuật, từ những ứng dụng đơn giản đến những hệ thống phức tạp. Dưới đây là một số ứng dụng nổi bật:

• Đồng hồ quả lắc: Đồng hồ quả lắc sử dụng dao động điều hòa của quả lắc để giữ thời gian. Sự chính xác của nó dựa trên chu kỳ dao động không đổi của quả lắc. Dùng trong đồng hồ treo tường, đồng hồ đứng cổ điển.
• Các hệ thống treo xe: Hệ thống treo của xe sử dụng lò xo và giảm xóc để hấp thụ xung lực từ mặt đường, tạo ra dao động điều hòa giúp cải thiện độ êm ái và ổn định cho xe. Dùng trong hầu hết các loại xe từ ô tô, xe máy đến xe đạp.
• Âm nhạc và âm thanh: Các nhạc cụ như đàn guitar, đàn piano, và kèn sử dụng dao động điều hòa của dây đàn hoặc cột không khí bên trong để tạo ra âm thanh. Dùng trong sản xuất âm nhạc, thiết kế âm thanh trong rạp hát và phòng thu.
• Kỹ thuật điện và điện tử: Các mạch dao động, bao gồm lò xo điện từ (cuộn cảm) và tụ điện, tạo ra dao động điều hòa dùng trong việc truyền và nhận tín hiệu. Ứng dụng trong điện thoại di động, radio, truyền hình, và các thiết bị viễn thông khác.
• Y học: Máy đo rung tim sử dụng dao động điều hòa để ghi lại hoạt động của tim, giúp phát hiện các bất thường. Nó có tác dụng chẩn đoán và theo dõi sức khỏe tim mạch.
• Kỹ thuật xây dựng: Tính toán dao động điều hòa giúp thiết kế các công trình có khả năng chịu đựng các rung động do gió, động đất, hoặc giao thông. Nó được ứng dụng trong việc làm cầu treo, tòa nhà chọc trời, đập nước.

Tóm lại, dao động điều hoà không chỉ là một chủ đề lý thú trong lĩnh vực vật lý mà còn có ảnh hưởng sâu rộng đến thế giới xung quanh chúng ta, từ cấu trúc của các công trình kiến trúc đến thiết kế của các thiết bị điện tử.

Việc hiểu biết sâu sắc về dao động điều hoà mở ra cánh cửa cho những tiến bộ kỹ thuật và công nghệ, nhấn mạnh tầm quan trọng của nó trong nghiên cứu và ứng dụng khoa học ngày nay.

Dao động điều hòa có mặt khắp nơi trong cuộc sống hàng ngày và trong nhiều lĩnh vực kỹ thuật, từ những ứng dụng đơn giản đến những hệ thống phức tạp. Dưới đây là một số ứng dụng nổi bật:

·         Đồng hồ quả lắc: Đồng hồ quả lắc sử dụng dao động điều hòa của quả lắc để giữ thời gian. Sự chính xác của nó dựa trên chu kỳ dao động không đổi của quả lắc. Dùng trong đồng hồ treo tường, đồng hồ đứng cổ điển.

·         Các hệ thống treo xe: Hệ thống treo của xe sử dụng lò xo và giảm xóc để hấp thụ xung lực từ mặt đường, tạo ra dao động điều hòa giúp cải thiện độ êm ái và ổn định cho xe. Dùng trong hầu hết các loại xe từ ô tô, xe máy đến xe đạp.

·         Âm nhạc và âm thanh: Các nhạc cụ như đàn guitar, đàn piano, và kèn sử dụng dao động điều hòa của dây đàn hoặc cột không khí bên trong để tạo ra âm thanh. Dùng trong sản xuất âm nhạc, thiết kế âm thanh trong rạp hát và phòng thu.

·         Kỹ thuật điện và điện tử: Các mạch dao động, bao gồm lò xo điện từ (cuộn cảm) và tụ điện, tạo ra dao động điều hòa dùng trong việc truyền và nhận tín hiệu. Ứng dụng trong điện thoại di động, radio, truyền hình, và các thiết bị viễn thông khác.

·         Y học: Máy đo rung tim sử dụng dao động điều hòa để ghi lại hoạt động của tim, giúp phát hiện các bất thường. Nó có tác dụng chẩn đoán và theo dõi sức khỏe tim mạch.

·         Kỹ thuật xây dựng: Tính toán dao động điều hòa giúp thiết kế các công trình có khả năng chịu đựng các rung động do gió, động đất, hoặc giao thông. Nó được ứng dụng trong việc làm cầu treo, tòa nhà chọc trời, đập nước.

Tóm lại, dao động điều hoà không chỉ là một chủ đề lý thú trong lĩnh vực vật lý mà còn có ảnh hưởng sâu rộng đến thế giới xung quanh chúng ta, từ cấu trúc của các công trình kiến trúc đến thiết kế của các thiết bị điện tử.

Việc hiểu biết sâu sắc về dao động điều hoà mở ra cánh cửa cho những tiến bộ kỹ thuật và công nghệ, nhấn mạnh tầm quan trọng của nó trong nghiên cứu và ứng dụng khoa học ngày nay.

Toán ạ

Bài 2: Viết các tích sau dưới dạng luỹ thừa, của một số tự nhiên.

a; a⁴.a⁶ = a⁴⁺⁶ = a¹⁰

b; (a⁵)⁷ = a⁵⁺⁷ = a¹² 

c; (a³)⁴.a⁹ = a¹².a⁹ = a¹²⁺⁹ = a²¹

d; (2³)⁵.(2³)⁴ = 2¹⁵.2¹² = 2¹⁵⁺¹² = 2²⁷

d) \(A=3cm\); \(\omega=4\pi\left(rad/s\right)\); \(\varphi_0=\dfrac{\pi}{5}\left(rad\right)\)

Khi đó \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)

Cho \(x=1,5cm\Leftrightarrow\varphi=\pm\dfrac{\pi}{3}\left(rad\right)\) 

Thời gian vật đi qua vị trí \(x=1,5cm\) lần thứ ba là:

\(T+t_d=0,5+\dfrac{\Delta\varphi_d}{2\pi}.T\)

\(=0,5+\dfrac{\dfrac{\pi}{3}-\dfrac{\pi}{5}}{2\pi}.0,5\)

\(=\dfrac{8}{15}\left(s\right)\)

e) Thời gian cần tìm là:

\(t_e+19T=\dfrac{\Delta\varphi_e}{2\pi}.T+19.0,5\) 

\(=\dfrac{\dfrac{4\pi}{3}}{2\pi}.0,5+9.5=\dfrac{59}{6}\left(s\right)\)