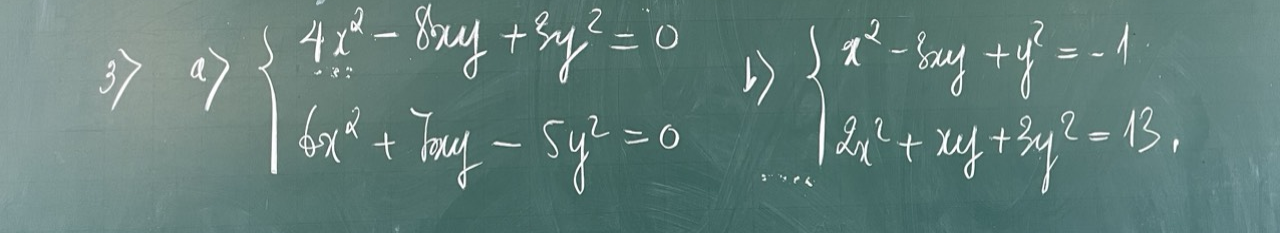a.

\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3y\right)\left(2x-y\right)=0\\6x^2+7xy-5y^2=0\end{matrix}\right.\)

TH1: \(2x-3y=0\Rightarrow y=\dfrac{2}{3}x\) thay vào pt dưới

\(\Rightarrow6x^2+7x.\left(\dfrac{2}{3}x\right)-5\left(\dfrac{2}{3}x\right)^2=0\)

\(\Leftrightarrow\dfrac{76}{9}x^2=0\Rightarrow x=0\Rightarrow y=0\)

TH2: \(2x-y=0\Rightarrow y=2x\)

Tương tự ta cũng được \(x=0;y=0\)

Vậy hệ có nghiệm duy nhất \(\left(x;y\right)=\left(0;0\right)\)

b.

\(\Leftrightarrow\left\{{}\begin{matrix}13x^2-39xy+13y^2=-13\\2x^2+xy+3y^2=13\end{matrix}\right.\)

Cộng vế với vế

\(\Rightarrow15x^2-38xy+16y^2=0\)

\(\Leftrightarrow\left(x-2y\right)\left(15x-8y\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=2y\\x=\dfrac{8}{15}y\end{matrix}\right.\)

Thay vào pt đầu:

- Với \(x=2y\Rightarrow4y^2-6y^2+y^2=-1\)

\(\Rightarrow y^2=1\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-1\Rightarrow x=-2\end{matrix}\right.\)

- Với \(x=\dfrac{8}{15}y\)

\(\Rightarrow\left(\dfrac{8}{15}y\right)^2-3\left(\dfrac{8}{15}y\right).y+y^2=-1\)

\(\Leftrightarrow-\dfrac{71}{225}y^2=-1\Rightarrow y^2=\dfrac{225}{71}\)

\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{15}{\sqrt{71}}\Rightarrow x=\dfrac{8}{\sqrt{71}}\\y=-\dfrac{15}{\sqrt{71}}\Rightarrow x=-\dfrac{8}{\sqrt{71}}\end{matrix}\right.\)

Em để ý thấy 2 số hạng đầu nếu đặt \(x\sqrt{x}\) làm nhân tử chung được: \(x\sqrt{x}\left(\sqrt{x}+1\right)\)

Giờ nó lại xuất hiện nhân tử \(\sqrt{x}+1\) với 2 số hạng cuối

Cứ vậy là ra thôi

Đề yêu cầu chứng minh hay tìm \(x;y\) vậy em nhỉ?

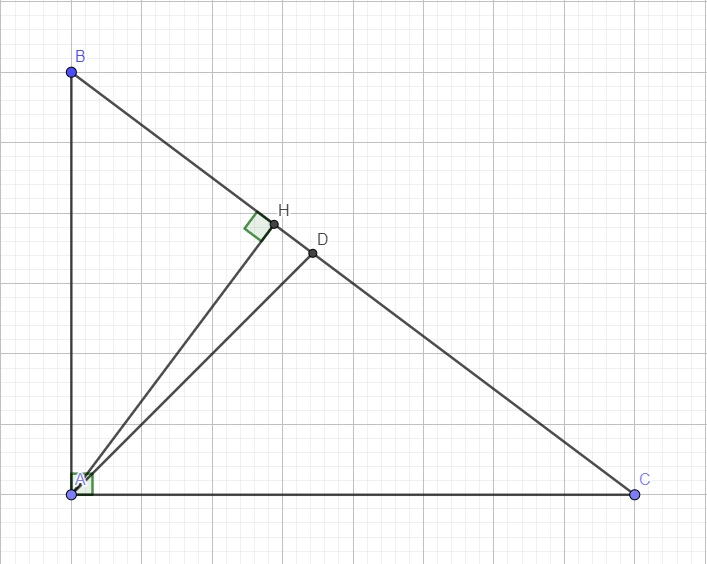
Ta có \(BC=BD+CD=35\left(cm\right)\)

Áp dụng định lý phân giác:

\(\dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{15}{20}=\dfrac{3}{4}\)

\(\Rightarrow AB=\dfrac{3}{4}AC\)

Áp dụng định lý Pitago:

\(AB^2+AC^2=BC^2\Rightarrow\dfrac{9}{16}AC^2+AC^2=35^2\)

\(\Rightarrow AC^2=784\Rightarrow AC=28\left(cm\right)\)

\(\Rightarrow AB=\dfrac{3}{4}AC=21\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác vuông ABC:

\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{63}{5}\left(cm\right)\)

\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\dfrac{84}{5}\left(cm\right)\)

\(HD=BD-BH=\dfrac{12}{5}\left(cm\right)\)

Áp dụng Pitago trong tam giác vuông ADH:

\(AD=\sqrt{AH^2+HD^2}=12\sqrt{2}\left(cm\right)\)

BD+CD=BC

=>BC=15+20=35(cm)

Xét ΔABC có AD là phân giác

nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)

=>\(\dfrac{AB}{15}=\dfrac{AC}{20}\)

=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=k\)

=>AB=3k; AC=4k

Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)

=>\(\left(3k\right)^2+\left(4k\right)^2=35^2\)

=>\(25k^2=1225\)

=>\(k^2=49\)

=>k=7

=>\(AB=3\cdot7=21\left(cm\right);AC=4\cdot7=28\left(cm\right)\)

Xét ΔABC có AD là phân giác

nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)

\(=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)

BD+CD=BC

=>BC=15+20=35(cm)

Xét ΔABC có AD là phân giác

nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)

=>\(\dfrac{AB}{15}=\dfrac{AC}{20}\)

=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=k\)

=>AB=3k; AC=4k

Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)

=>\(\left(3k\right)^2+\left(4k\right)^2=35^2\)

=>\(25k^2=1225\)

=>\(k^2=49\)

=>k=7

=>\(AB=3\cdot7=21\left(cm\right);AC=4\cdot7=28\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH\cdot BC=AB\cdot AC\)

=>\(AH=\dfrac{21\cdot28}{35}=21\cdot\dfrac{4}{5}=16,8\left(cm\right)\)

a: Để hệ có nghiệm duy nhất thì \(\dfrac{3}{m}\ne\dfrac{-1}{1}=-1\)

=>\(m\ne-3\)

b: Để hệ vô nghiệm thì \(\dfrac{3}{m}=\dfrac{-1}{1}\ne\dfrac{6}{n+3}\)

=>\(\left\{{}\begin{matrix}m=-3\\n+3\ne-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-3\\n\ne-9\end{matrix}\right.\)

c: Để hệ có vô số nghiệm thì \(\dfrac{3}{m}=\dfrac{-1}{1}=\dfrac{6}{n+3}\)

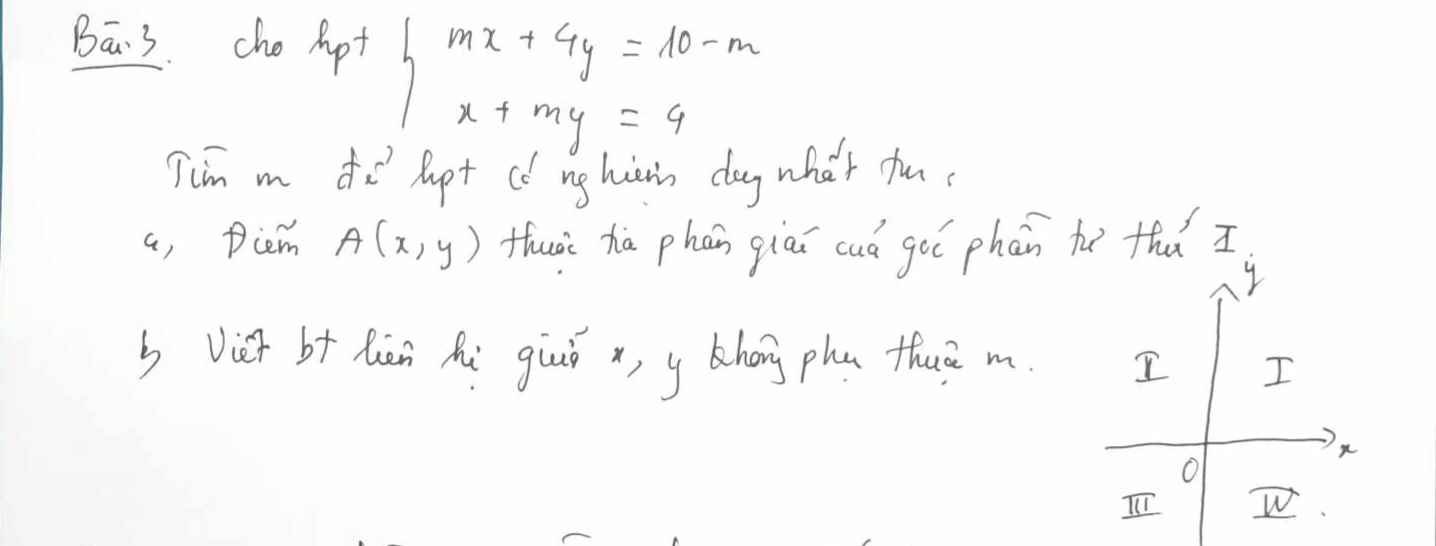
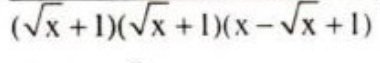
=>\(\left\{{}\begin{matrix}m=-3\\n+3=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-3\\n=-9\end{matrix}\right.\)