Đặt C=1.2.3+2.3.4+3.4.5+4.5.6+...+98.99.100

4C=(1.2.3+2.3.4+3.4.5+4.5.6+...+98.99.100)4

4C=1.2.3(4-0)+2.3.4(5-1)+3.4.5(6-2)+4.5.6(7-3)+...+98.99.100(101-97)

4C=1.2.3.4+2.3.4.5-1.2.3.4+3.4.5.6-2.3.4.5+4.5.6.7-3.4.5.6+...+98.99.100.101-97.98.99.100

4C=1.2.3.4-1.2.3.4+2.3.4.5-2.3.4.5+3.4.5.6-3.4.5.6+...+97.98.99.100-97.98.99.100+98.99.100.101

4C=98.99.100.101

=>C=98.99.100.101/4

TK nhé

** Bổ sung điều kiện $a,b,c,d>0$

Lời giải:
Đặt biểu thức đã cho là $A$.

Với $a,b,c,d>0$ thì:

$A>\frac{a}{a+b+c+d}+\frac{b}{a+b+c+d}+\frac{c}{a+b+c+d}+\frac{d}{a+b+c+d}=1(*)$

Mặt khác:
Xét hiệu:

$\frac{a}{a+b+c}-\frac{a+d}{a+b+c+d}=\frac{-(bd+dc)}{(a+b+c)(a+b+c+d)}<0$ với $a,b,c,d>0$

$\Rightarrow \frac{a}{a+b+c}< \frac{a+d}{a+b+c+d}$

Hoàn toàn tương tự ta cũng có:

$\frac{b}{a+b+d}< \frac{b+c}{a+b+c+d}$

$\frac{c}{b+c+d}< \frac{c+a}{a+b+c+d}$

$\frac{d}{a+c+d}< \frac{d+b}{a+b+c+d}$

Cộng theo vế các BĐT trên thì:
$A< \frac{a+d+b+c+c+a+d+b}{a+b+c+d}=\frac{2(a+b+c+d)}{a+b+c+d}=2(**)$

Từ $(*); (**)\Rightarrow 1< A< 2$

$\Rightarrow A$ không là số tự nhiên.

Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

ta có : (x-13+y)²⁰²⁴+(x-6-y)²⁰²⁴=0

do (x-13+y)²⁰²⁴ ≥ 0 ∀ x,y 

(x-6-y)²⁰²⁴  ≥ 0 ∀ x,y

⇒ (x-13+y)²⁰²⁴+(x-6-y)²⁰²⁴ ≥ 0

Dấu "=" xảy ra khi x-13+y=0 

                              x-6-y=0

⇔ x+y = 13   (1)

     x-y =6       (2)

Từ (1) và (2) suy ra x=9,5   và y = 3,5 

Vậy .... 

x = 0 

y = 1

gợi ý

x hoặc xy = 1 hoặc -1

(mik ko bt lắm chỉ gợi ý đc thôi)

Bài 1:

Vì $M$ là trung điểm của $AB$ nên:

$MA=MB=\frac{AB}{2}=\frac{2}{2}=1$ (cm)

Bài 2: Bạn xem lại đề. Oa nằm giữa Oa và Ob? Tại sao phải tính số đo góc $\widehat{aOc}$ khi đã biết nó bằng $30^0$ như đề đã đề cập?

1 + 1 = 2

1+1=2

       Đây là dạng toán nâng cao chuyên đề tổng hiệu lồng nhau, cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay olm.vn sẽ hướng dẫn em giải chi tiết dạng này như sau:

                     Giải

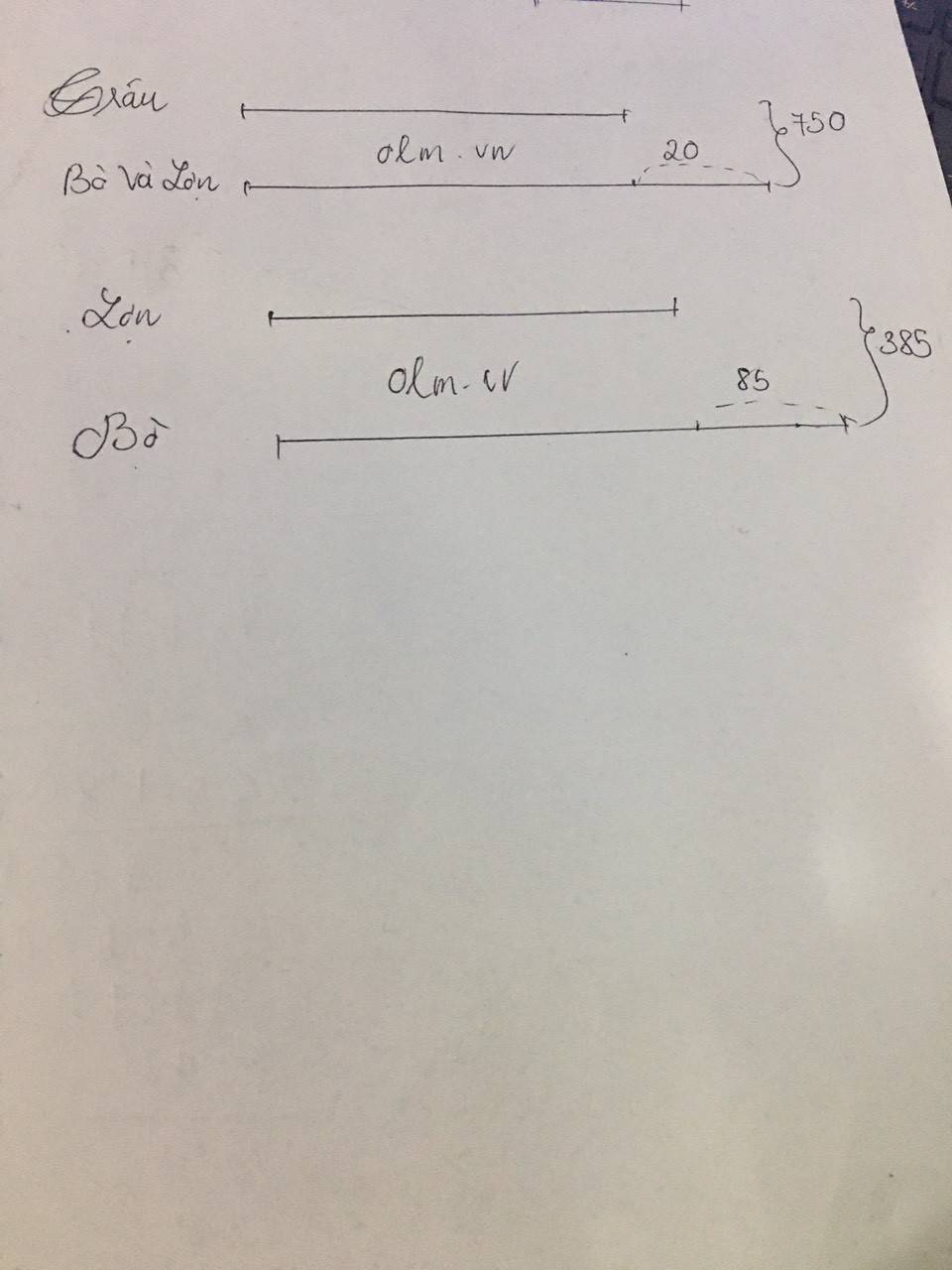
Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có:

Trâu nặng số ki-lô-gam là: (750 - 20): 2 = 365 (kg)

Tổng số ki-lô-gam của bò và lợn là: 750 - 365 = 385 (kg)

Ta có sơ đồ:

Lợn nặng số ki-lô-gan là:

(385 - 85): 2  = 150 (kg)

Bò nặng số ki-lô-gam là: 385 - 150 = 235 (kg)

Đáp số: 235 kg 

a) Xét △ABC vuông tại A nên: AB² + AC² = BC² (Định lí Pythagore)
suy ra BC = \(\sqrt{AB^2+AC^2}\)

                 = \(\sqrt{6^2+8^2}\)

                 = 10
Vậy BC = 10

a: Sửa đề: AB=6

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(\)\(BC^2=6^2+8^2=100=10^2\)

=>BC=10

b: Sửa đề: tính BD,CD

Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{6}=\dfrac{DC}{8}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

mà DB+DC=BC=10

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)

=>\(DB=3\cdot\dfrac{10}{7}=\dfrac{30}{7};DC=4\cdot\dfrac{10}{7}=\dfrac{40}{7}\)

5a/

$A=\frac{1}{2^2}(1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{50^2})$

$=\frac{1}{4}(1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+....+\frac{1}{50^2})$

$< \frac{1}{4}(1+\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{49.50})$

$=\frac{1}{4}(1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{49}-\frac{1}{50})$

$=\frac{1}{4}(2-\frac{1}{50})< \frac{1}{4}.2=\frac{1}{2}$

5b/

Gọi $d=ƯCLN(2m+3, m+1)$

$\Rightarrow 2m+3\vdots d; m+1\vdots d$

$\Rightarrow 2m+3-2(m+1)\vdots d$

$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $2m+3, m+1$ nguyên tố cùng nhau. Do đó $\frac{2m+3}{m+1}$ là phân số tối giản.

Lời giải:

$A=1-\frac{1}{2}+1-\frac{1}{6}+1-\frac{1}{12}+1-\frac{1}{20}+.....+1-\frac{1}{240}$

$=\underbrace{(1+1+....+1)}_{15}-(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+....+\frac{1}{240})$

$=15-(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{15.16})$

$=15-(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{15}-\frac{1}{16})$

$=15-(1-\frac{1}{16})=\frac{225}{16}$

$\Rightarrow a=225; b=16\Rightarrow a-b=209$

$