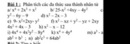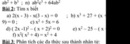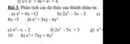\(1:a,x^4+2x^3+x^2\)

\(x^2\left(x^2+2x+1\right)\)

\(x^2\left(x+1\right)^2\)

\(\left(x^2+x\right)^2\)

\(b,25-x^2+4xy-4y^2\)

\(5^2-\left(x-2y\right)^2\)

\(\left(5-x+2y\right)\left(5+x-2y\right)\)

\(c,y^2-6y-9\)

\(\left(y-3\right)^2-18\)

\(\left(y-3\right)^2-\sqrt{18}^2=\left(y-3-3\sqrt{2}\right)\left(y-3+3\sqrt{2}\right)\)

\(d,x^2-2x-3\)

\(x^2-2x+1-4\)

\(\left(x-1\right)^2-2^2=\left(x-1-2\right)\left(x-1+2\right)\)

\(\left(x-3\right)\left(x+1\right)\)

\(e,9-x^2+2xy-y^2\)

\(9-\left(x^2-2xy+y^2\right)=9-\left(x-y\right)^2\)

\(\left(3-x+y\right)\left(3+x-y\right)\)

\(f,x^2-xz+y^2-yz+2xy\)

\(\left(x+y\right)^2-xz-yz\)

\(\left(x+y\right)^2-z\left(x+y\right)\)

\(\left(x+y\right)\left(x+y-z\right)\)

\(g,4x^2+4x-3\)

\(4x^2+4x+1-4\)

\(\left(x+1\right)^2-2^2=\left(x+1-2\right)\left(x+1+2\right)\)

\(\left(x-1\right)\left(x+3\right)\)

\(h,x^2-x-12\)

\(x^2-x+\frac{1}{2}-\frac{25}{2}\)

\(\left(x-\frac{1}{2}\right)^2-\left(\frac{5}{\sqrt{2}}\right)^2\)

\(\left(x-\frac{1}{2}-\frac{5}{\sqrt{2}}\right)\left(x-\frac{1}{2}+\frac{5}{\sqrt{2}}\right)\)

\(\left(x-\frac{1+5\sqrt{2}}{2}\right)\left(x-\frac{1-5\sqrt{2}}{2}\right)\)

\(i,4x^4+4x^2y^2-8y^4\)

\(\left(2x^2\right)^2+4x^2y^2+\left(y^2\right)^2-\left(3y^2\right)^2\)

\(\left(2x^2+y^2\right)^2-\left(3y^2\right)^2\)

\(\left(2x^2+y^2-3y^2\right)\left(2x^2+y^2+3y^2\right)=\left(2x^2-2y^2\right)\left(2x^2+4y^2\right)\)

\(k,x^4+4y^4\)

\(\left(x^2\right)^2+4x^2y^2+\left(2y^2\right)^2-4x^2y^2\)

\(\left(x^2+2y^2\right)^2-\left(2xy\right)^2\)

\(\left(x^2+2y^2-2xy\right)\left(x^2+2y^2+2xy\right)\)

\(l,ab^2+b^3\)

\(b^2\left(a+b\right)\)

\(m,a^3-a\)

\(a\left(a^2-1\right)\)

\(a\left(a-1\right)\left(a+1\right)\)

\(n,ab^2c^3+64ab^2\)

\(ab^2\left(c^3+64\right)\)

\(ab^2\left(c^3+4^3\right)\)

\(ab^2\left(c+4\right)\left(c^2+4c+16\right)\)

Trả lời:

\(A=\frac{5}{x^2-x+1}=\frac{5}{x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}}=\frac{5}{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}}\)

Ta có: \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\forall x\)

\(\Leftrightarrow\frac{5}{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}}\le\frac{5}{\frac{3}{4}}\forall x\)

\(\Leftrightarrow A\le\frac{20}{3}\forall x\)

Dấu "=" xảy ra khi \(x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}\)

Vậy GTLN của A bằng 20/3 khi x = 1/2

a) (7x - 8)(7x + 8) - 10(2x + 3)² + 5x(3x - 2)² - 4x(x - 5)²

= 49x² - 64 - 10(4x² + 12x + 9) + 5x(9x² - 12x + 4)  - 4x(x²  - 10x + 25)

= 49x² - 64 - 40x² - 120x - 90 + 45x³ - 60x² + 20x - 4x³ + 40x - 100x

= 41x³ - 51x² - 160x - 154

b) (x2 - 3)(x² + 3) - 5x²(x + 1)² - (x² - 3x)(x² - 2x) + 4x(x + 2)²

= x⁴ - 9 - 5x2(x² + 2x + 1) - x⁴ + 5x³ - 6x² + 4x(x² + 4x + 4)

= 5x³ - 6x² - 5x⁴ - 10x³ - 5x² + 4x³ + 16x² + 16x - 9

= -5x⁴ - x³ + 5x² + 16x - 9

Trả lời:

a , ( 7x - 8 ) ( 7x + 8 ) - 10 ( 2x + 3 )² + 5x ( 3x - 2 )² - 4x ( x - 5 )²

= 49x² - 64 - 10 ( 4x² + 12x + 9 ) + 5x ( 9x² - 12x + 4 ) - 4x ( x² - 10x + 25 )

= 49x² - 64 - 40x² + 120x - 90 + 45x³ - 60x² + 20x - 4x³ + 40x² - 100x

= 41x³ - 11x² + 40x - 154

b , ( x² - 3 ) ( x² + 3 ) - 5x² ( x + 1 )² - ( x² - 3x ) ( x² - 2x ) + 4x ( x + 2 )²

= x⁴ - 9 - 5x² ( x² + 2x + 1 ) - ( x⁴ - 2x³ - 3x³ + 6x² ) + 4x ( x² + 4x + 4 )

= x⁴ - 9 - 5x⁴ - 10x³ - 5x² - x⁴ + 2x³ + 3x³ - 6x² + 4x³ + 16x² + 16x

= - 5x⁴ - x³ + 5x² + 16x - 9

ấy nhầm

Ta có M = x² - 6x + 8 = x² - 6x + 9 - 1 = (x - 3)² - 1 \(\ge-1\)

Dấu "=" xảy ra <=> x - 3= 0 

<=> x = 3

Vậy Min M = -1 <=> x = 3

Trả lời:

\(M=x^2-6x+8=\left(x^2-2.x.3+3^2\right)-1=\left(x-3\right)^2-1\)

Ta có: \(\left(x-3\right)^2\ge0\forall x\)

\(\Leftrightarrow\left(x-3\right)^2-1\ge-1\forall x\)

Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3

Vậy GTNN của M = - 1 khi x = 3

x³ + 3x = 3x² + 1

<=> x³ - 3x² + 3x - 1 = 0

<=> (x - 1)³ = 0

<=> x - 1 = 0

<=> x  = 1

Vậy x = 1 là nghiệm phương trình

Trả lời:

x³ + 3x = 3x² + 1

<=> x³ + 3x - 3x² - 1 = 0

<=> ( x - 1 )³ = 0

<=> x - 1 = 0 

<=> x = 1

Vậy S = { 1 }

\(x=b+c-a,y=a+c-b,z=a+b-c\)

\(x^3+y^3+z^3=\left(x+y+z\right)^3-3\left(x+y\right)\left(y+z\right)\left(z+x\right)\)

\(=\left(a+b+c\right)^3-3.2c.2a.2b\)

\(=\left(a+b+c\right)^3-24abc\)

\(\left(a+b+c\right)^3-x^3-y^3-z^3=\left(a+b+c\right)^3-\left[\left(a+b+c\right)^3-24abc\right]=24abc\)

sửa lại đề bài \(3.3^{3n-1}\left(6.3^{n+2}+3\right)-2.3^n\left(3^{n+3}-1\right)=405\)

\(3^n\left(6.3.3.3^n+3\right)-2.3^n\left(3.3.3.3^n-1\right)=405\)

\(3^n\left(54.3^n+3\right)-2.3^n\left(27.3^n-1\right)=405\)

\(54.3^{2n}+3.3^n-54.3^{2n}+2.3^n=405\)

\(5.3^n=405\)

\(3^n=81\)

\(< =>n=4\)

vậy n =4

Bài 3:

a) \(M=\left(x+y\right)^3+2x^2+4xy+2y^2=\left(x+y\right)^3+2\left(x+y\right)^2=7^3+2.7^2=441\)

b) \(N=\left(x-y\right)^3-x^2+2xy-y^2=\left(x-y\right)^3-\left(x^2-2xy+y^2\right)=\left(x-y\right)^3-\left(x-y\right)^2\)

\(=\left(-5\right)^3-\left(-5\right)^2=-150\)

Bài 4: 

a) \(M=4x^2+8x+7=4x^2+8x+4+3=4\left(x+1\right)^2+3\ge3\)

Dấu \(=\)khi \(x+1=0\Leftrightarrow x=-1\).

b) \(N=6x-x^2-7=-\left(x^2-6x+9\right)+2=-\left(x-3\right)^2+2\le2\)

Dấu \(=\)khi \(x-3=0\Leftrightarrow x=3\).