cho đường tròn tâm o ,dây ab không đi qua tâm , dây mn vuông góc với ab tại h (ah>bh),i là hình chiếu của m trên nb , k là giao điểm của mi và ab .a) chubgws minh b,h,m,i thuộc 1 đường tròn .b)chứng minh tâm giác mak cân .c) chứng minh mi×ma=mh×mn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cảm ơn em đã phản hồi tới olm.vn. Vấn đề em hỏi olm xin trả lời như sau. Hiện tại chính sách olm đã thay đổi. Với mỗi câu trả lời đúng và được giáo viên tick xanh thì chỉ được gp thôi em nhé. Bạn nào đứng top đầu bảng xếp hạng thì cuối tuần sẽ được olm trao xu, xu em có thể đổi quà trên shop của olm. olm đã check câu trả lời của em thì em mới trả lời một câu và cũng chưa được giáo viên nào chấm bài cả em nhé! Nên tất nhiên em chưa thể có xu của olm. Vì xu chỉ trao cho bạn có nhiều gp nhất vào cuối tuần.


Lời giải:
Gọi số lọ sát khuẩn 2 lớp điều chế được ngày thứ nhất lần lượt là $a,b$. Theo bài ra ta có:
$a+b=110$
$1,25a+1,2b=135$
Giải hệ phương trình gồm 2 PT trên thu được: $a=60; b=50$ (lọ)

số tự nhiên bé nhất mà lập phương số đó có chữ số cuối bên phải là chữ số là số: 17

\(\dfrac{25112012}{11}=2282911-\dfrac{9}{11}\Rightarrow a=2282911\)
\(\dfrac{9}{11}=\dfrac{1}{\dfrac{11}{9}}=\dfrac{1}{1+\dfrac{2}{9}}=\dfrac{1}{1+\dfrac{1}{\dfrac{9}{2}}}=\dfrac{1}{1+\dfrac{1}{4+\dfrac{1}{2}}}\)
\(\Rightarrow b=1;c=4;d=2\)

Áp dụng BĐT AM-GM ta có
x^3/1+y +1+y/4+1/2 >= 3 căn 3(x^3/8) =3x/2
Tương tự: y^3/1+z + 1+z/4 +1/2 >= 3z/2
z^3/1+x +1+x/4 + 1/2 >= 3z/2
=> P + x+y+z+3/4 +3/2 >= 3(x+y+z)/2
<=> P >= [5(x+y+z)-3]/4 -3/2
<=> P >= 5(x+y+z)/4 -9/4
Mặt khác x+y+z>=xy+yz+zx>=3
( bạn tự chứng minh nhé)
=> P>= 15/4 -9/4=3/2
=>P >=3/2
Dấu = xảy ra khi x=y=z=1
Nhớ tick cho mình nhé
Áp dụng BĐT AM-GM ta có
x^3/1+y +1+y/4+1/2 >= 3 căn 3(x^3/8) =3x/2
Tương tự: y^3/1+z + 1+z/4 +1/2 >= 3z/2
z^3/1+x +1+x/4 + 1/2 >= 3z/2
=> P + x+y+z+3/4 +3/2 >= 3(x+y+z)/2
<=> P >= [5(x+y+z)-3]/4 -3/2
<=> P >= 5(x+y+z)/4 -9/4
Mặt khác x+y+z>=xy+yz+zx>=3
( bạn tự chứng minh nhé)
=> P>= 15/4 -9/4=3/2
=>P >=3/2
Dấu = xảy ra khi x=y=z=1
Nhớ tick cho mình nhé

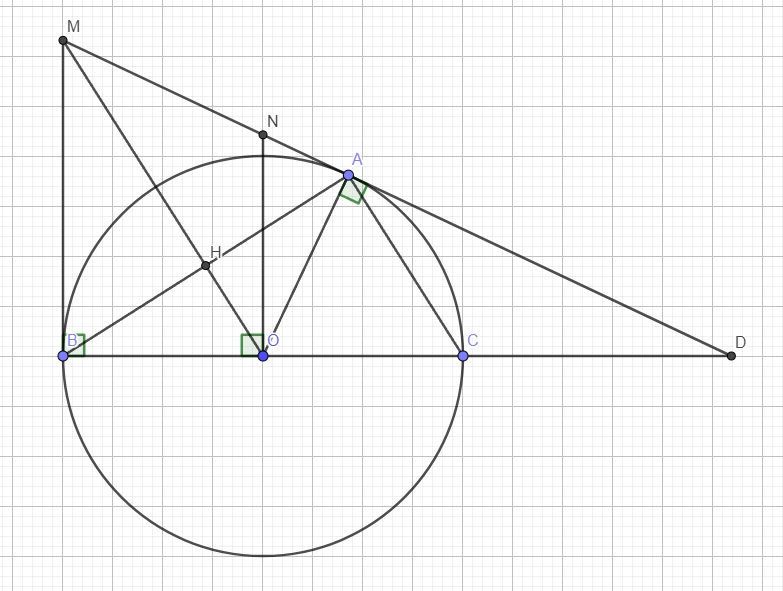
4c.
Do M là giao điểm 2 tiếp tuyến tại A và B, theo tính chất hai tiếp tuyến cắt nhau
\(\Rightarrow\widehat{OMN}=\widehat{OMB}\)
Mà \(MB||NO\) (cùng vuông góc BC) \(\Rightarrow\widehat{OMB}=\widehat{MON}\) (so le trong)
\(\Rightarrow\widehat{OMN}=\widehat{MON}\)
\(\Rightarrow\Delta OMN\) cân tại N
\(\Rightarrow MN=ON\)
Cũng theo 2 t/c 2 tiếp tuyến cắt nhau \(\Rightarrow MA=MB\)
Do MD là tiếp tuyến của (O) tại A \(\Rightarrow OA\perp MD\)
Áp dụng hệ thức lượng trong tam giác vuông OND với đường cao OA:
\(ON^2=NA.ND\Rightarrow MN^2=NA.ND\)
\(\Rightarrow MN^2=\left(MA-MN\right).ND=\left(MB-MN\right).ND\)
\(\Rightarrow MN^2=MB.ND-MN.ND\)
\(\Rightarrow MB.ND-MN^2=MN.ND\)
\(\Rightarrow\dfrac{MB.ND-MN^2}{MN.ND}=1\)
\(\Rightarrow\dfrac{MB}{MN}-\dfrac{MN}{ND}=1\) (đpcm)
 Tại sao em trả lời trong thời gian trên mà không được COIN ạ ?
Tại sao em trả lời trong thời gian trên mà không được COIN ạ ?
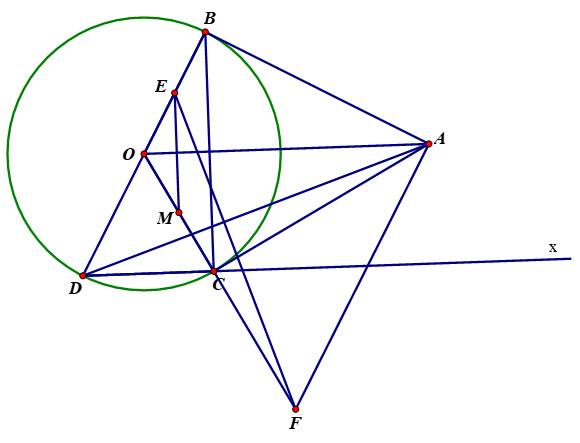

a/
Ta có
\(AB\perp MN\left(gt\right)\Rightarrow\widehat{MHB}=90^o\)
\(MI\perp BN\Rightarrow\widehat{MIB}=90^o\)
=> H và I cùng nhìn MB dưới 1 góc \(90^o\) => H; I thuộc đường tròn đường kính MB => B; H; M; I cùng thuộc 1 đường tròn
b/
Xét tg vuông MHK và tg vuông MIN có
\(\widehat{MKA}=\widehat{MNI}\) (cùng phụ với \(\widehat{KMN}\) )
Ta có
\(\widehat{MNI}=\widehat{MAK}\) (góc nội tiếp cùng chắn cung MB)
\(\Rightarrow\widehat{MKA}=\widehat{MAK}\) => tg MAK cân tại M
c/
Xét tg vuông MIN và tg vuông MHK có
\(\widehat{MKA}=\widehat{MNI}\) (cmt)
=> tg MNI đồng dạng với MHK (g.g.g)
\(\Rightarrow\dfrac{MI}{MH}=\dfrac{MN}{MK}\)
Ta có tg MAK cân tại M (cmt) => MK=MA
\(\Rightarrow\dfrac{MI}{MH}=\dfrac{MN}{MA}\Rightarrow MI.MA=MH.MN\)