Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có : \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)^3-3\left(a+b\right)c\left(a+b+c\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left[\left(a+b+c\right)^2-3\left(a+b\right)c-3ab\right]=0\)
(luôn đúng ,do \(a+b+c=0\))
b) Ta có : \(\left(a+b+c\right)^2=3\left(a^2+b^2+c^2\right)\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=3\left(a^2+b^2+c^2\right)\)
\(\Rightarrow2\left(a^2+b^2+c^2\right)=2\left(ab+bc+ca\right)\)
\(\Rightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\)
\(\Rightarrow a=b=c\)
c) Ta có : \(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=3\left(ab+bc+ca\right)\)
\(\Rightarrow a^2+b^2+c^2=ab+bc+ca\)
\(\Rightarrow2a^2+2b^2+2c^2=2ab+2bc+2ca\)
\(\Rightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\)
\(\Rightarrow a=b=c\)
Áp dụng bất đẳng thức Co-si cho hai số không âm ta có:
\(x+y\ge2\sqrt{xy}\)
\(y+z\ge2\sqrt{yz}\)
\(z+x\ge2\sqrt{zx}\)
\(\Rightarrow\left(x+y\right)\left(y+z\right)\left(z+x\right)\ge8\sqrt{\left(xyz\right)^2}=8xyz\)
Dấu "=" <=> x = y = z. (đpcm)
Bạn tham khảo ở phần câu hỏi tương tự nhé.
Câu hỏi của đậu xanh vlog - Toán lớp 8 - Học trực tuyến OLM
a)\(9x^2+30x+16=0\)
\(< =>9x^2+24x+6x+16=0\)
\(< =>3x.\left(3x+8\right)+2.\left(3x+8\right)=0\)
\(< =>\left(3x+2\right).\left(3x+8\right)=0\)
\(< =>\orbr{\begin{cases}3x+2=0\\3x+8=0\end{cases}< =>\orbr{\begin{cases}x=\frac{-2}{3}\\x=\frac{-8}{3}\end{cases}}}\)
Vậy S={-2/3;-8/3}
9x2 + 30x + 16 = 0 <=> 9x2 + 24x + 6x + 16 = 0
<=> 3x( 3x + 8 ) + 2( 3x + 8 ) = 0 <=> ( 3x + 8 )( 3x + 2 ) = 0
<=> x = -8/3 hoặc x = -2/3
b) 8x3 - 36x2 + 54x - 28 = 0
<=> 8x3 - 16x2 - 20x2 + 40x + 14x - 28 = 0
<=> 8x2( x - 2 ) - 20x( x - 2 ) + 14( x - 2 ) = 0
<=> ( x - 2 )( 8x2 - 20x + 14 ) = 0
Vì 8x2 - 20x + 14 = 8( x - 5/4 )2 + 3/2 > 0 ∀ x
=> x - 2 = 0 <=> x = 2
2) \(P=\frac{4}{2x^2+2xy+y^2+5x+20}=\frac{4}{\left(x^2+2xy+y^2\right)+\left(x^2+5x+\frac{25}{4}\right)+\frac{75}{4}}\)
\(=\frac{4}{\left(x+y\right)^2+\left(x+\frac{5}{2}\right)^2+\frac{75}{4}}\)
Để P đạt GTLN
=> Mẫu thức đạt GTNN
mà \(\left(x+y\right)^2+\left(x+\frac{5}{2}\right)^2+\frac{75}{4}\ge\frac{75}{4}\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+y=0\\x+\frac{5}{2}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-\frac{5}{2}\\y=\frac{5}{2}\end{cases}}\)
Thay x = -5/2 và y = 5/2 vào P
Khi đó P = \(\frac{4}{\left(-\frac{5}{2}+\frac{5}{2}\right)^2+\left(-\frac{5}{2}+\frac{5}{2}\right)^2+\frac{75}{4}}=\frac{4}{\frac{75}{4}}=\frac{16}{75}\)
Vậy Max P = 16/75 <=> x = -5/2 ; y = 5/2
1) Ta có P = x2 + 2xy + 3y2 + 5y + 10
= (x2 + 2xy + y2) + (2y2 + 5y + 10)
= \(\left(x+y\right)^2+2\left(y^2+\frac{5}{2}y+5\right)=\left(x+y\right)^2+2\left(y^2+\frac{5}{2}y+\frac{25}{16}+\frac{55}{16}\right)\)
= \(\left(x+y\right)^2+2\left(y+\frac{5}{4}\right)^2+\frac{55}{8}\ge\frac{55}{8}\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+y=0\\y+\frac{5}{4}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{4}\\y=-\frac{5}{4}\end{cases}}\)
Vạy Min P = 55/8 <=> x = 5/4 ; y = -5/4
( 2x + 1 )2 - 4( 2x + 1 ) + 4 = 16
<=> ( 2x + 1 - 2 )2 - 16 = 0
<=> ( 2x - 1 )2 - 42 = 0
<=> ( 2x - 1 - 4 )( 2x - 1 + 4 ) = 0
<=> ( 2x - 5 )( 2x + 3 ) = 0
<=> x = 5/2 hoặc x = -3/2
Ta có : a5 - a = a( a4 - 1 ) = a( a2 - 1 )( a2 + 1 )
= a( a - 1 )( a + 1 )( a2 - 4 + 5 )
= a( a - 1 )( a + 1 )[ ( a - 2 )( a + 2 ) + 5 ]
= 5a( a - 1 )( a + 1 ) + a( a - 1 )( a + 1 )( a - 2 )( a + 2 )
Dễ chứng minh \(\hept{\begin{cases}5a\left(a-1\right)\left(a+1\right)⋮30\\a\left(a-1\right)\left(a+1\right)\left(a-2\right)\left(a+2\right)⋮30\end{cases}}\)=> 5a( a - 1 )( a + 1 ) + a( a - 1 )( a + 1 )( a - 2 )( a + 2 ) ⋮ 30
hay a5 - a ⋮ 30 ( đpcm )
Ta có:\(a^5-a=a\left(a^4-1\right)=a\left(a^2-1\right)\left(a^2+1\right)=a\left(a-1\right)\left(a+1\right)\left(a^2+1\right)\)
Vì \(\left(a-1\right)a\)là tích của 2 số tự nhiên liên tiếp nên chia hết cho2
\(\left(a-1\right)a\left(a+1\right)\)là tích của 3 số tự nhiên liên tiếp nên chia hết cho 3
Mà \(\left(2,3\right)=1\)\(\Rightarrow a\left(a-1\right)\left(a+1\right)\left(a^2+1\right)⋮\left(2.3\right)=6\)
Nếu \(a=5q\left(q\in N\right)\Rightarrow a\left(a-1\right)\left(a+1\right)\left(a^2+1\right)⋮5\)
Nếu \(a=5q+1\Rightarrow a-1=5q\)
Nếu \(a=5q+2\Rightarrow a^2+1=\left(5q+2\right)^2+1=25q^2+5\)
Nếu \(a=5q+3\Rightarrow a^2+1=\left(5q+3\right)^2+1=25q^2+10\)
Nếu \(a=5q+4\Rightarrow a+1=5q+4+1=5q+5\)
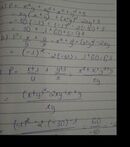
gọi công suất dự định là x
thời gian dự định là \(\frac{60}{x}\)
thời gian bơm nửa bể lúc đầu là \(\frac{30}{x}\)
thời gian bơm nửa bể lúc sau là \(\frac{30}{x-3}\)
\(30p=\frac{1}{2}h\)
ta có pt:
\(\frac{30}{x}+\frac{30}{x-3}-\frac{60}{x}=\frac{1}{2}\)
\(60x\left(x-3\right)+60x^2-120x\left(x-3\right)=x^2\left(x-3\right)\)
\(60x^2-180x+60x^2-120x^2+360x=x^3-3x^2\)
\(180x=x^3-3x^2\)
\(x^3-3x^2-180x=0\)
\(x\left(x^2-3x-180\right)=0\)
\(\orbr{\begin{cases}x=0\\\left(x^2-3x-180\right)=0\end{cases}\orbr{\begin{cases}x=0\left(KTM\right)\\\sqrt{\Delta}=27\end{cases}}}\)
\(\orbr{\begin{cases}x_1=\frac{3+27}{2}=15\left(TM\right)\\x_2=\frac{3-27}{2}=-12\left(KTM\right)\end{cases}}\)
vậy .......... công suất dự kiến ban đầu là 15 m3/h