với a,b,c là các số thực thỏa mãn a^3+b^3+c^3=4abc và ab+2bc+3ca=0, chứng minh rằng a=b=c=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KN
1
AH
Akai Haruma
Giáo viên
27 tháng 1
Lời giải:
$A=x^3+y^3+xy=(x+y)^3-3xy(x+y)+xy$
$=1-3xy+xy=1-2xy=(x+y)^2-2xy=x^2+y^2$
Áp dụng BĐT Cô-si:
$x^2+\frac{1}{4}\geq x$
$y^2+\frac{1}{4}\geq y$
$\Rightarrow A=x^2+y^2\geq x+y-\frac{1}{2}=1-\frac{1}{2}=\frac{1}{2}$
Vậy $A_{\min}=\frac{1}{2}$
Giá trị này đạt tại $x=y=\frac{1}{2}$
26 tháng 1
Đó là kí hiệu tích nhé bạn.
VD1: Cho n số thực \(a_1,a_2,...,a_n\) thì kí hiệu:
\(\prod\limits^n_{i=1}a_i=a_1.a_2...a_n\)
VD2: Cho n số thực dương \(a_1,a_2,...,a_n\). Khi đó ta có bất đẳng thức Cô-si nổi tiếng:
\(\dfrac{a_1+a_2+...+a_n}{n}\ge\sqrt[n]{a_1a_2...a_n}\)
Sử dụng kí hiệu, ta có thể viết lại BĐT này như sau:
\(\dfrac{\sum\limits^n_{i=1}a_i}{n}\ge\sqrt[n]{\prod\limits^n_{i=1}a_i}\). Ta thấy kí hiệu \(\prod\) xuất hiện ở vế phải làm cho BĐT trở nên gọn gàng hơn rất nhiều.
H9
HT.Phong (9A5)
CTVHS
24 tháng 1
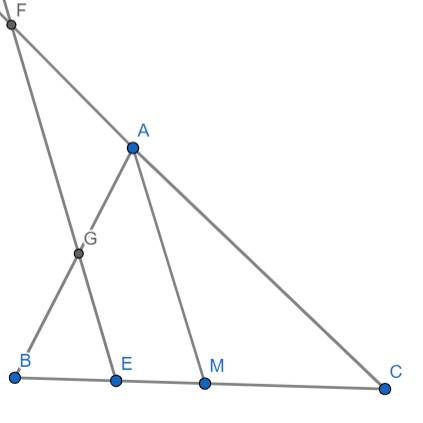
Ta có: \(EF//AM\left(gt\right)\)
\(\Rightarrow\widehat{FEC}=\widehat{AMC}\) (đồng vị)
Xét hai tam giác FEC và AMC có:
\(\widehat{FCE}\) chung
\(\widehat{FEC}=\widehat{AMC}\) (cmt)
\(\Rightarrow\Delta FEC\sim\Delta AMC\) (g.g)
\(\Rightarrow\dfrac{EF}{AM}=\dfrac{CE}{CM}\Rightarrow\dfrac{CM}{AM}=\dfrac{CE}{EF}\) (1)
Chứng minh tương tự ta có: \(\Delta BEG\sim\Delta BMA\left(g.g\right)\)
\(\Rightarrow\dfrac{EG}{AM}=\dfrac{BE}{BM}\Rightarrow\dfrac{CM}{AM}=\dfrac{BE}{EG}\) (vì \(CM=BM\)) (2)
Từ (1) và (2) ta có:
\(\dfrac{CE}{EF}=\dfrac{BE}{EG}\Rightarrow EG\cdot CE=EF\cdot BE\)
\(\Rightarrow EG\cdot\left(BC-BE\right)=EF\cdot BE\)
\(\Rightarrow EG\cdot BC-EG\cdot BE=EF\cdot BE\)
\(\Rightarrow EF\cdot BE+EG\cdot BE=EG\cdot BC\)
\(\Rightarrow EF+EG=\dfrac{EG\cdot BC}{BE}\left(3\right)\)
Từ (2) ta có: \(\dfrac{EG}{AM}=\dfrac{BE}{BM}\)
\(\Rightarrow BM\cdot EG=BE\cdot AM\Rightarrow\dfrac{1}{2}BC\cdot EG=BE\cdot AM\)
\(\Rightarrow EG\cdot BC=2AM\cdot BE\)
\(\Rightarrow2AM=\dfrac{EG\cdot BC}{BE}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow EF+EG=2AM\) (đpcm)