di chuyển Hai Que Diêm 19 + 17 = 24 cứu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


B = - \(\dfrac{5}{2}\) - \(\dfrac{2}{3}\) \(\sqrt{\dfrac{x}{2}+3}\)
B = - (\(\dfrac{5}{2}\) + \(\dfrac{2}{3}\)\(\sqrt{\dfrac{x}{2}+3}\)) (đk \(\dfrac{x}{2}\) + 3 ≥ 0 ⇒ \(x\) ≥ - 6)
\(\sqrt{\dfrac{x}{2}+3}\) ≥ 0
⇒ \(\dfrac{2}{3}\)\(\sqrt{\dfrac{x}{2}+3}\) ≥ 0
⇒ \(\dfrac{5}{2}+\dfrac{2}{3}\sqrt{\dfrac{x}{2}+3}\) ≥ \(\dfrac{5}{2}\)
⇒ -(\(\dfrac{5}{2}\) + \(\dfrac{2}{3}\)\(\sqrt{\dfrac{x}{2}+3}\)) ≤ - \(\dfrac{5}{2}\)
Vậy Bmax = - \(\dfrac{5}{2}\) khi \(\sqrt{\dfrac{x}{2}+3}\) = 0 ⇒ \(\dfrac{x}{2}\) + 3 = 0 ⇒ \(\dfrac{x}{2}\) = -3; ⇒ \(x=-6\)
Kết luận: Giá trị lớn nhất của biểu thức là - \(\dfrac{5}{2}\) xảy ra khi \(x=-6\)

Sửa đề: cắt BC lần lượt tại E và F
a: Ta có: E nằm trên đường trung trực của AB
=>EA=EB
=>ΔEAB cân tại E
b: D nằm trên đường trung trực của AC
=>DA=DC
F nằm trên đường trung trực của AC
=>FC=FA
Xét ΔADF và ΔCDF có
DA=DC
DF chung
FA=FC
Do đó: ΔADF=ΔCDF

A B C D E F M N
a/ Xét tg ABE có
\(DM\perp AB\Rightarrow EM\perp AB\)
=> tg ABE cân tại E (Tam giác có đường cao đồng thời là đường trunbg trực thì tg đó là tg cân)
b/
Xét tg ACF, chứng minh tương tự câu a => tg ACF cân tại F
=> AF = CF (1)
Xét tg ACD, chứng minh tương tự => tg ACD cân tại D
=> AD = CD (2)
Xét tg ADF và tg CDF có
DF chung (3)
Từ (1) (2) (3) => tg ADF = tg CDF (c.c.c)
c/
Xét tg ABD, chứng minh tương tự câu a => tg ABD cân tại D
\(\Rightarrow\widehat{ABD}=\widehat{BAD}\)
Ta có tg ACD cân (cmt) \(\Rightarrow\widehat{CAD}=\widehat{ACD}\)
\(\Rightarrow\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=120^o=\widehat{ABD}+\widehat{ACD}\)
Xét tứ giác ABDC có
\(\widehat{BDC}=360^o-\widehat{BAC}-\left(\widehat{ABD}+\widehat{ACD}\right)\) (Tổng các góc trong của 1 tứ giác bằng \(360^o\))
\(\Rightarrow\widehat{BDC}=360^o-120^o-120^o=120^o\)
Ta có
tg ABD cân tại D (cmt) => AD = BD
tg ACD cân tại D (cmt) => AD = CD
=> BD = CD => tg BCD cân tại D \(\Rightarrow\widehat{CBD}=\widehat{BCD}\) (4)
Xét tg cân BCD có
\(\widehat{CBD}+\widehat{BCD}=180^o-\widehat{BDC}=180^o-120^o=60^o\) (5)
Từ (4) và (5) \(\Rightarrow\widehat{CBD}=\widehat{BCD}=\dfrac{60^o}{2}=30^o\)
Chứng minh tương tự câu b => tg DE = tg BDE (c.c.c)
\(\Rightarrow\widehat{EAD}=\widehat{CBD}=30^o\)

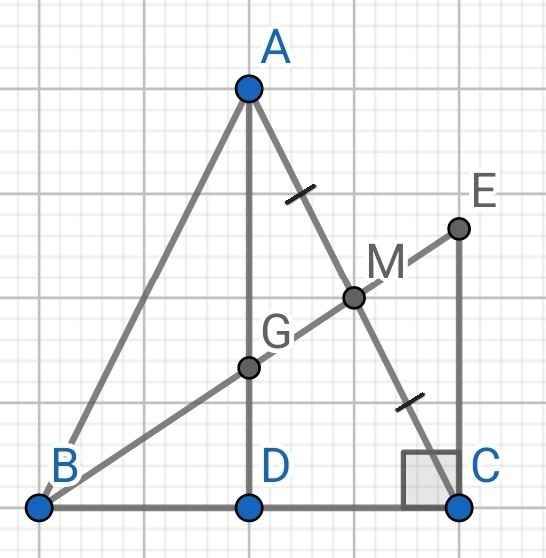
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Do AD là đường phân giác của ∆ABC (gt)
⇒ ∠BAD = ∠CAD
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
b) ∆ABC cân tại A (gt)
AD là đường phân giác (gt)
⇒ AD cũng là đường cao của ∆ABC
⇒ AD ⊥ BC
c) Do CE ⊥ BC (gt)
AD ⊥ BC (cmt)
⇒ AD // CE
⇒ ∠GAM = ∠ECM (so le trong)
Do BM là đường trung tuyến của ∆ABC (gt)
⇒ M là trung điểm của AC
⇒ AM = CM
Xét ∆AGM và ∆CEM có:
∠GAM = ∠ECM (cmt)
AM = CM (cmt)
∠AMG = ∠CME (đối đỉnh)
⇒ ∆AGM = ∆CEM (g-c-g)

\(2x^3+7x^2+ax+3⋮x^2+2x+1\)
=>\(2x^3+4x^2+2x+3x^2+6x+3+\left(a-8\right)x⋮x^2+2x+1\)
=>a-8=0
=>a=8

\(\dfrac{1+5y}{5x}=\dfrac{1+4y}{4x}\) (\(x\ne\) 0)
\(\dfrac{1}{5x}\) + \(\dfrac{y}{x}\) = \(\dfrac{1}{4x}\) + \(\dfrac{y}{x}\)
\(\dfrac{1}{5x}\) = \(\dfrac{1}{4x}\)
\(\dfrac{1}{5x}-\dfrac{1}{4x}=0\)
\(\dfrac{4-5}{20x}\) = 0
\(\dfrac{1}{20x}\) = 0 (vô lí)
Kết luận: Phương trình đã cho vô nghiệm

Đề đọc khó hiểu quá. Các ký hiệu thiếu tùm lum không à. Bạn xem lại nhé.

Trên tia đối của tia NB, lấy E sao cho NB=NE
Xét ΔNBC và ΔNEA có
NB=NE
\(\widehat{BNC}=\widehat{ENA}\)(hai góc đối đỉnh)
NC=NA
Do đó: ΔNBC=ΔNEA
=>EC=EA
Xét ΔCBE có CB+CE>EB
mà CE=BA và EB=2BN
nên CB+BA>2BN

Lời giải:
Nếu $x>2001$ thì:
$A=x-2001+x-1=2x-2002> 2.2001-2002=2000$
Nếu $1\leq x\leq 2001$:
$A=2001-x+x-1=2000$
Nếu $x< 1$ thì:
$A=2001-x+1-x=2002-2x> 2002-2.1=2000$
Từ 3 TH trên suy ra $A_{\min}=2000$. Giá trị này đạt được khi $1\leq x\leq 2000$
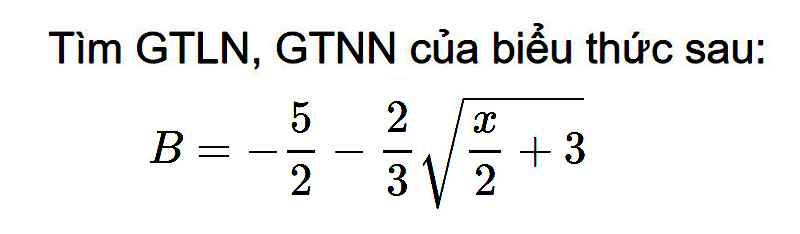
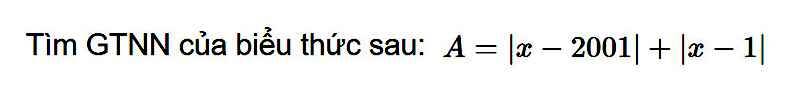
Em phải viết số theo đúng với đề bài thì mới biết vị trí của que diêm để di chuyển chứ em?
k thấy ảnh bn nha! xem lại đề ạ
#hoctot