M = 7 + 7² + 7³ + 7⁴ + 7⁵ + 7⁶ + 7⁷ + 7⁸

M = (7 + 7²) + (7³ + 7⁴) + (7⁵ + 7⁶) + (7⁷ + 7⁸)

M = 7.(1 + 7) + 7³.(1+ 7) + 7⁵.(1 + 7)  + 7⁷.(1 + 7)

M = (1 + 7).(7 + 7³ + 7⁵+ 7⁷)

M = 8.(7 + 7³ + 7⁵ + 7⁷) ⋮ 2

M là số chẵn 

M = 7 + 7² + 7³ + 7⁴ + 7⁵ + 7⁶ + 7⁷ + 7⁸

M = (7 + 7³) + (7² + 7⁴) + (7⁵ + 7⁷) + (7⁶ + 7⁸)

M = 7.(1 + 7²) + 7².(1 + 7²) + 7⁵.(1 + 7²) + 7⁶.(1 + 7²)

M = (1 + 7²).(7 + 7²+ 7⁵ +  7⁶)

M  =(1+  49).(7 + 7² + 7⁵+ 7⁶)

M =  50.(7 + 7² + 7⁵ +  7⁶)  (vậy M chia hết cho 5)

M =  \(\overline{..0}\) (M có tận cùng bằng 0

M = 7 + 7² + 7³ + 7⁴ + 7⁵ + 7⁶ + 7⁷ + 7⁸

M = (7 + 7²) + (7³ + 7⁴) + (7⁵ + 7⁶) + (7⁷ + 7⁸)

M = 7.(1 + 7) + 7³.(1+ 7) + 7⁵.(1 + 7)  + 7⁷.(1 + 7)

M = (1 + 7).(7 + 7³ + 7⁵+ 7⁷)

M = 8.(7 + 7³ + 7⁵ + 7⁷) ⋮ 2

M là số chẵn 

SOS

`15/12 -(-5/13) - 3/12 - 18/13`

` = 15/12 + 5/13 - 3/12 - 18/13`

` = (15/12 - 3/12) + (5/13 - 18/13)`

`= 1 + -1`

`= 0`

`a,` Mỗi ngày, tổng số tiền góp của cả hai bạn là:

`5000 . 2 = 10000 (` đồng `)`

Sau `10` ngày, tổng số tiền góp được là:

`10000 . 10 = 100000 (` đồng `)`

`b,` Ngày thứ `2`, mỗi bạn góp `5000` đồng.

Ngày thứ `3`, mỗi bạn góp gấp đôi ngày trước là `5000 . 2 = 10000 (` đồng `)`

Ngày thứ `4`, mỗi bạn góp gấp đôi ngày trước là: `10000 . 2 = 20000 (` đồng `)`

Ngày thứ `5`, mỗi bạn góp gấp đôi ngày trước là: `20000 . 2 = 40000 (` đồng `)`

Biểu thức tổng số tiền của mộtbạn sau ngày thứ năm là: `5000 . 2^0 + 5000 . 2^1 + 5000 . 2^2 + 5000 .  2^3 + 5000 . 2^4 (` đồng `)`

Biểu thức tổng số tiền của cả hai bạn sau ngày thứ năm là:`2 . [5000 . (2^0 + 2^1 + 2^2 + 2^3 + 2^4)] (` đồng `)`

2^\(2+x\) + 2^\(x\)  = 80

2^\(x\).2² + 2^\(x\) = 80

2\(^x\).(2² + 1) =  80

2\(^x\).(4 + 1) = 80

2\(^x\).5 = 80

2\(^x\)     = 80 : 5

2\(^x\)     = 16

2\(^x\)     = 2⁴

\(x=4\)

Vậy \(x=4\)

\(2^{x+2}+2^x=80\)

=>\(4\cdot2^x+2^x=80\)

=>\(5\cdot2^x=80\)

=>\(2^x=\dfrac{80}{5}=16=2^4\)

=>x=4

\(56-22\left(x+3\right)^3=2\)

=>\(22\left(x+3\right)^3=56-2=54\)

=>\(\left(x+3\right)^3=\dfrac{54}{22}=\dfrac{27}{11}\)

=>\(x+3=\dfrac{3}{\sqrt[3]{11}}\)

=>\(x=\dfrac{3\sqrt[3]{121}}{121}-3=\dfrac{3\sqrt[3]{121}-363}{121}\)

Chép đúng đề chưa em, lớp sáu chưa học căn em ơi?

A  =5 + 5² + 5³ + ... + 5¹⁰⁰

A ⋮ 1; 5 ; A (A > 5)

Vậy A là hợp số

b; A = 5 + 5² + 5³ + ... + 5¹⁰⁰

   A =  5 + 5²(1 + 5  + 5² + ... + 5⁹⁸)

 ⇒  A \(⋮\) 5; A không chia hết cho 5². Vậy A không phải là số chính phương vì số chính phương chia hết cho một số nguyên tố thì phải chia hết cho bình phương số nguyên tố đó. 

a) 9x²(2x - 3) = 0

9x² = 0 hoặc 2x - 3 = 0

*) 9x² = 0

x² = 0

x = 0

*) 2x - 3 = 0

2x = 3

Vậy:

b; (4\(x+2\))(\(x^2\) + 1) = 0

     \(x^2\) ≥ 0 ⇒ \(x^2\) + 1 ≥ 1 ∀ \(x\)

 ⇒   4\(x+2\) = 0  ⇒ 4\(x=-2\) ⇒ \(x=-\dfrac{1}{2}\)

Vậy \(x=-\dfrac{1}{2}\) 

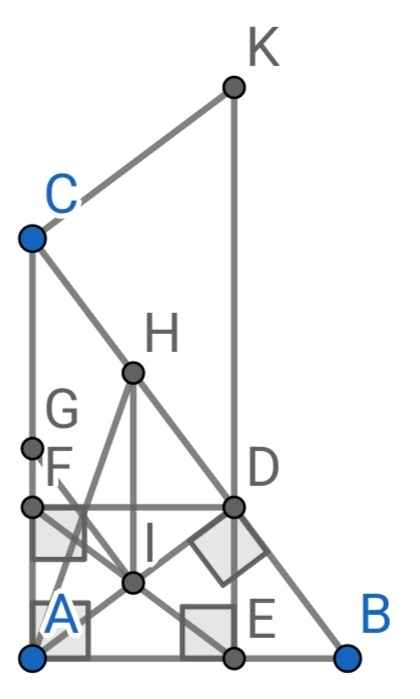
a) ∆ABC vuông tại A (gt)

⇒ AB ⊥ AC

⇒ ∠CAB = 90⁰

⇒ ∠EAF = 90⁰

Do E, F là hình chiếu của D lên AB, AC (gt)

⇒ ∠AED = ∠AFD = 90⁰

Tứ giác AEDF có:

∠EAF = ∠AED = ∠AFD = 90⁰ 

⇒ AEDF là hình chữ nhật

b) Do I là giao điểm của EF và AD (gt)

⇒ I là trung điểm của AD

Lại có:

H là trung điểm của DC (gt)

⇒ IH là đường trung bình của ∆ACD

⇒ IH // AC và IH = AC : 2

Do G là trung điểm của AC (gt)

⇒ CG = AC : 2

⇒ IH = CG = AC : 2

Do IH // AC (cmt)

⇒ IH // AG

Tứ giác IHCG có:

IH // CG (cmt)

IH = CG (cmt)

⇒ IHCG là hình bình hành

c) Do E là hình chiếu của D lên AB (gt)

⇒ DE ⊥ AB

Mà AC ⊥ AB (cmt)

⇒ DE // AC

⇒ DK // AC

Tứ giác ADKC có:

DK // AC (cmt)

DK = AC (gt)

⇒ ADKC là hình bình hành

⇒ CK // AD

d) Do IH // CG (cmt)

⇒ IH // AC

Mà AC ⊥ AB (cmt)

⇒ IH ⊥ AB

⇒ HI là đường cao của ∆HAB

Do AD là đường cao của ∆ABC (gt)

⇒ AD ⊥ BC

⇒ AD ⊥ BH

⇒ AD là đường cao của ∆HAB

∆HAB có:

HI là đường cao (cmt)

AD là đường cao thứ hai (cmt)

Mà I là giao điểm của HI và AD

⇒ I là giao điểm của ba đường cao của ∆HAB

⇒ I là trực tâm của ∆HAB