ai giúp e với ạ e cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(C=x^2+x-2\)
\(=x^2+2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2-2-\left(\frac{1}{2}\right)^2\)
\(=\left(x+\frac{1}{2}\right)^2-\frac{9}{4}\)
Mà\(\left(x+\frac{1}{2}\right)^2\ge0\Rightarrow\left(x+\frac{1}{2}\right)^2-\frac{9}{4}\ge-\frac{9}{4}\)
Vậy \(C_{Min}=-\frac{9}{4}\)khi và chỉ khi\(\left(x+\frac{1}{2}\right)^2=0\Leftrightarrow x=-\frac{1}{2}\)
b)
\(D=x^2+y^2+x-6y+5\)
\(=x^2+2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+y^2-2.y.3+3^2+5-\left(\frac{1}{2}\right)^2-3^2\)
\(=\left(x+\frac{1}{2}\right)^2+\left(y-3\right)^2-\frac{17}{4}\)
Mà\(\left(x+\frac{1}{2}\right)^2+\left(y-3\right)^2\ge0\Rightarrow\left(x+\frac{1}{2}\right)^2+\left(y-3\right)^2-\frac{17}{4}\ge-\frac{17}{4}\)
Vậy \(D_{Min}=-\frac{17}{4}\)khi và chỉ khi \(\hept{\begin{cases}\left(x+\frac{1}{2}\right)^2=0\\\left(y-3\right)^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-\frac{1}{2}\\y=3\end{cases}}\)
c)
\(E=x^2+10y^2-6xy-10y+26\)
\(=x^2-2.x.3y+\left(3y\right)^2+y^2-2.y.5+5^2+26-5^2\)
\(=\left(x-3y\right)^2+\left(y-5\right)^2+1\)
Mà\(\left(x-3y\right)^2+\left(y-5\right)^2\ge0\Rightarrow\left(x-3y\right)^2+\left(y-5\right)^2+1\ge1\)
Vậy \(E_{Min}=1\)khi và chỉ khi\(\hept{\begin{cases}\left(x-3y\right)^2=0\\\left(y-5\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=15\\y=5\end{cases}}}\)


a, \(E=4x^2+6x+5=4\left(x^2+\frac{2.3}{4}x+\frac{9}{16}-\frac{9}{16}\right)+5\)
\(=4\left(x+\frac{3}{4}\right)^2+\frac{11}{4}\ge\frac{11}{4}>0\forall x\)
Vậy ta có đpcm
b, \(F=2x^2-3x+7=2\left(x^2-\frac{2.3}{4}x+\frac{9}{16}-\frac{9}{16}\right)+7\)
\(=2\left(x-\frac{3}{4}\right)^2+\frac{47}{8}\ge\frac{47}{8}>0\forall x\)
Vậy ta có đpcm
c, \(K=5x^2-4x+1=5\left(x^2-\frac{2.2}{5}x+\frac{4}{25}-\frac{4}{25}\right)+1\)
\(=5\left(x-\frac{2}{5}\right)^2+\frac{1}{5}\ge\frac{1}{5}>0\forall x\)
Vậy ta có đpcm
d, \(Q=3x^2+2x+5=3\left(x^2+\frac{2}{3}x+\frac{1}{9}-\frac{1}{9}\right)+5\)
\(=3\left(x+\frac{1}{3}\right)^2+\frac{14}{3}\ge\frac{14}{3}>0\forall x\)
Vậy ta có đpcm

= 5
hehe, easy game :)) (ko biết đúng hay sai đâu, mk sủa thế cho vui)
Hok tốt


Áp dụng BĐT Cauchy Schwarz dạng Engel
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{\left(1+1+1\right)^2}{a+b+c}=\frac{9}{a+b+c}\)
Dấu ''='' xảy ra khi a = b = c

rút gọn
a. ( x-2)^3- x(x+1)(x-1)+ 6x(x-3)
= -5x-8
b.(x-2)(x^2-2x+4)(x+2)(x^2+2x+4)
= x^6-64
nha bạn chúc bạn học tốt ạ
( x - 2 )3 - x( x + 1 )( x - 1 ) + 6x( x - 3 )
= x3 - 6x2 + 12x - 8 - x( x2 - 1 ) + 6x2 - 18x
= x3 - 6x - 8 - x3 + x
= -5x - 8

Trong cách sử dụng thông thường, tuyến tính được dùng để nói lên một mối quan hệ toán học hoặc hàm có thể được biểu diễn trên đồ thị là một đường thẳng, như trong hai đại lượng tỉ lệ thuận với nhau, chẳng hạn như điện áp và dòng điện trong một mạch RLC, hoặc khối lượng và trọng lượng của một vật.
tuyến tính được dùng để nói lên một mối quan hệ toán học hoặc hàm có thể được biểu diễn trên đồ thị là một đường thẳng, như trong hai đại lượng tỉ lệ thuận với nhau, chẳng hạn như điện áp và dòng điện trong một mạch RLC, hoặc khối lượng và trọng lượng của một vật.
mạng ă
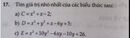
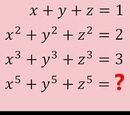
\(\left(\frac{x^2-3x}{x^2-9}-1\right):\left(\frac{9-x^2}{x^2+x-6}-\frac{x-3}{2-x}-\frac{x-2}{x+3}\right)\)
\(=\left(\frac{x^2-3x}{x^2-9}-1\right):\left(\frac{9-x^2}{x^2+x-6}+\frac{x-3}{x-2}-\frac{x-2}{x+3}\right)\)
\(=\left(\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-1\right):\left(\frac{\left(3-x\right)\left(3+x\right)}{x^2+x-6}+\frac{\left(x-3\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}-\frac{\left(x-2\right)^2}{\left(x+3\right)\left(x-2\right)}\right)\)
\(=\left(\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-1\right):\left(\frac{\left(3-x\right)\left(3+x\right)}{x^2+x-6}+\frac{\left(x-3\right)\left(x+3\right)-\left(x-2\right)^2}{x^2+x-6}\right)\)
\(=\left(\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\frac{9-x^2+x^2-9-x^2+4x-4}{x^2+x-6}\)
\(=\frac{x\left(x-3\right)-\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}:\frac{-\left(x-2\right)^2}{x^2+x-6}\)
\(=\frac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}:\frac{-\left(x-2\right)^2}{x^2+x-6}\)
\(=\frac{3}{x+3}.\frac{x^2+x-6}{-\left(x-2\right)^2}\)
\(=\frac{3}{x+3}.\frac{\left(x+3\right)\left(x-2\right)}{-\left(x-2\right)^2}\)
\(=\frac{3}{2-x}\)
HT