Giải phương trình x^3-7x^2+11x-4+2√(x-1)^3=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(ĐKXĐ:x\ne1;x\ge0\)
\(P=\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{\sqrt{x}+1}{x-1}\)
\(P=\frac{x+2+\sqrt{x}+1\left(x-1\right)-\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}{\left(x+\sqrt{x}+1\right)\left(x-1\right)}\)
\(P=\frac{x+2+x\sqrt{x}+x-\sqrt{x}-1-x\sqrt{x}-x-x-\sqrt{x}-\sqrt{x}-1}{\left(x+\sqrt{x}+1\right)\left(x-1\right)}\)
\(P=\frac{-3\sqrt{x}}{x\sqrt{x}-1}\)

Xét tam giác \(BGA\)vuông tại \(G\):
\(BA^2=BG^2+GA^2=\frac{4}{9}\left(BE^2+AM^2\right)\Leftrightarrow BE^2+\frac{BC^2}{4}=\frac{27}{2}\)(1)
Xét tam giác \(ABE\)vuông tại \(A\):
\(BE^2=AB^2+AE^2=6+\frac{1}{4}AC^2\)(2)
Từ (1) và (2) suy ra \(BC^2+AC^2=30\)
mà \(BC^2=AC^2+6\)
suy ra \(BC^2=18\Rightarrow BC=3\sqrt{2}\left(cm\right)\).

\(AB^2=BH.BC=HB.\left(HB+HC\right)=HB^2+15HB\)
\(\Leftrightarrow HB^2+15HB=16\Leftrightarrow HB=1\left(cm\right)\)

\(AB^2=BH.BC=\frac{1}{5}BC.BC\)
\(\Rightarrow BC=\sqrt{5AB^2}=10\left(cm\right)\)

Ko đăng linh tinh lên diễn đàn
Đây ko phải là toán

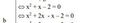
Trên mạng nó thế
\(x^3-7x^2+11x-4+2\sqrt{\left(x-1\right)^3}=0\) (ĐK: \(x\ge1\))
\(\Leftrightarrow\left(x-1\right)^3-4\left(x-1\right)^2+2\sqrt{\left(x-1\right)^3}+1=0\)
Đặt \(t=\sqrt{x-1}\ge0\)
Phương trình ban đầu tương đương với:
\(t^6-4t^4+2t^3+1=0\)
\(\Leftrightarrow\left(t^3+1\right)^2-\left(2t^2\right)^2=0\)
\(\Leftrightarrow\left(t^3-2t^2+1\right)\left(t^3+2t^2+1\right)=0\)
\(\Leftrightarrow t^3-2t^2+1=0\)(vì \(t^3+2t^2+1>0\))
\(\Leftrightarrow\left(t-1\right)\left(t^2-t-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=1\\t=\frac{1+\sqrt{5}}{2}\end{cases}}\)(vì \(t\ge0\))
\(\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{5+\sqrt{5}}{2}\end{cases}}\)(thỏa mãn)