25%-1và 1/2-(-1/2)^2+0,25÷1/1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{4}{3}\)x+x-\(\dfrac{5}{2}\)x=9
\(\dfrac{-1}{6}\)x=9
x=9*(-6)
x=-54

Lời giải:
$A=1+2+2^2+...+2^{2021}+2^{2022}$
$2A=2+2^2+2^3+...+2^{2022}+2^{2023}$
$2A-A=2+2^2+2^3+...+2^{2022}+2^{2023}-(1+2+2^2+...+2^{2021}+2^{2022})$
$\Rightarrow A=2^{2023}-1$
Ta thấy:
$2\equiv -1\pmod 3\Rightarrow A=2^{2023}-1\equiv (-1)^{2023}-1\equiv 1\pmod 3(1)$
Mặt khác:
$2^3\equiv 1\pmod 7\Rightarrow 2^{2023}=(2^3)^{674}.2\equiv 1^{674}.2\equiv 2\pmod 7$
$\Rightarrow A=2^{2023}-1\equiv 2-1\equiv 1\pmod 7(2)$
Từ $(1); (2)$ mà $(3,7)=1$ nên $A\equiv 1\pmod {3.7}$ hay $A\equiv 1\pmod {21}$
Vậy $A$ chia $21$ dư $1$
Ta có: \(A=2^0+2^1+2^2+...+2^{2021}+2^{2022}\)
\(=>2A=2^1+2^2+2^3+...+2^{2022}+2^{2023}\)
\(2A-A=\left(2^1+2^2+2^3+...+2^{2022}+2^{2023}\right)-\left(2^0+2^1+2^2+...+2^{2021}+2^{2022}\right)\)
\(A=2^{2023}-2^0=2^{2023}-1\)
Ta lại có: \(2^6=64\equiv1\left(mod21\right),2^{2023}=\left(2^6\right)^{337}.2\equiv1^{337}.2=1.2=2\left(mod21\right) =>2^{2023}-1=2-1=1\left(mod21\right)\)
=> A chia 21 dư 1. Vậy A chia 21 dư 1

Xin lỗi bn mik ko bt làm:))))))
Thành thật sorry bn:)))




\(\dfrac{1}{2!}+\dfrac{2}{3!}+\dfrac{3}{4!}+...+\dfrac{n}{\left(n+1\right)!}\)
\(=\dfrac{2-1}{2!}+\dfrac{3-1}{3!}+\dfrac{4-1}{4!}+...+\dfrac{\left(n+1\right)-1}{\left(n+1\right)!}\)
\(=\dfrac{2}{2!}-\dfrac{1}{2!}+\dfrac{3}{3!}-\dfrac{1}{3!}+...+\dfrac{\left(n+1\right)}{\left(n+1\right)!}-\dfrac{1}{\left(n+1\right)!}\)
\(=1-\dfrac{1}{2!}+\dfrac{1}{2!}-\dfrac{1}{3!}+\dfrac{1}{3!}+...+\dfrac{1}{n!}-\dfrac{1}{\left(n+1\right)!}\)
( Vì \(\dfrac{3}{3!}=\dfrac{1}{2!};\dfrac{4}{4!}=\dfrac{1}{3!};...;\dfrac{n+1}{\left(n+1\right)!}=\dfrac{1}{n!}\))
\(=1-\dfrac{1}{\left(n+1\right)!}< 1\)
Đặt \(S\left(n\right)=\dfrac{1}{2!}+\dfrac{2}{3!}+\dfrac{3}{4!}+...+\dfrac{n}{\left(n+1\right)!}\)
Ta có \(S\left(1\right)=\dfrac{1}{2!}=\dfrac{1}{2}=1-\dfrac{1}{2!}\)
\(S\left(2\right)=S\left(1\right)+\dfrac{2}{3!}=\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}=1-\dfrac{1}{3!}\)
\(S\left(3\right)=S\left(2\right)+\dfrac{3}{4!}=\dfrac{5}{6}+\dfrac{1}{8}=\dfrac{23}{24}=1-\dfrac{1}{4!}\)
Từ đây, ta có \(S\left(n\right)=1-\dfrac{1}{\left(n+1\right)!}\) và hiển nhiên \(S\left(n\right)< 1\) do \(\dfrac{1}{\left(n+1\right)!}>0\)
Vậy ta có đpcm
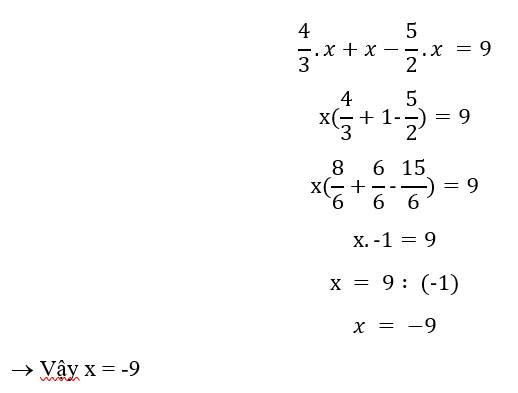
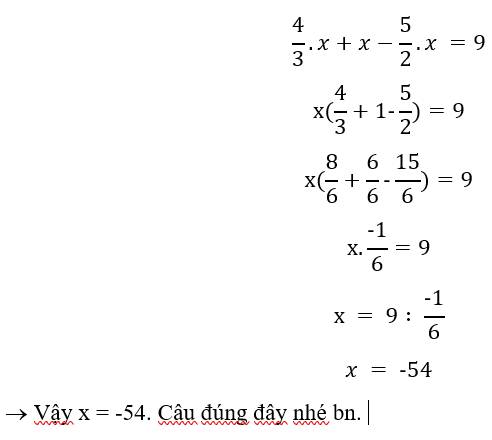

\(25\%-1=\dfrac{1}{4}-1=\dfrac{1-4}{4}=-\dfrac{3}{4}\\ \\= \dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}:1=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{4}{1}=\dfrac{2-1+16}{4}=\dfrac{1}{2}\)