em khong biet

Bạn nhân chéo rồi rút gọn thì được:

\(x^4-3x^3+3x+1=0\\ \Leftrightarrow(x^2-2x-1)(x^2-x-1)=0\)

Bạn tự giải tiếp nhé.

GDgfdsgdfggdffdv

Ta có thể dùng cosy hoặc đặt a,b lần lượt là hai số hạng vế trái của phương, đưa phương trình về hệ phương trình không triệt để. Từ đó giải phương.

Đầu kiện: \(x\ge0\)

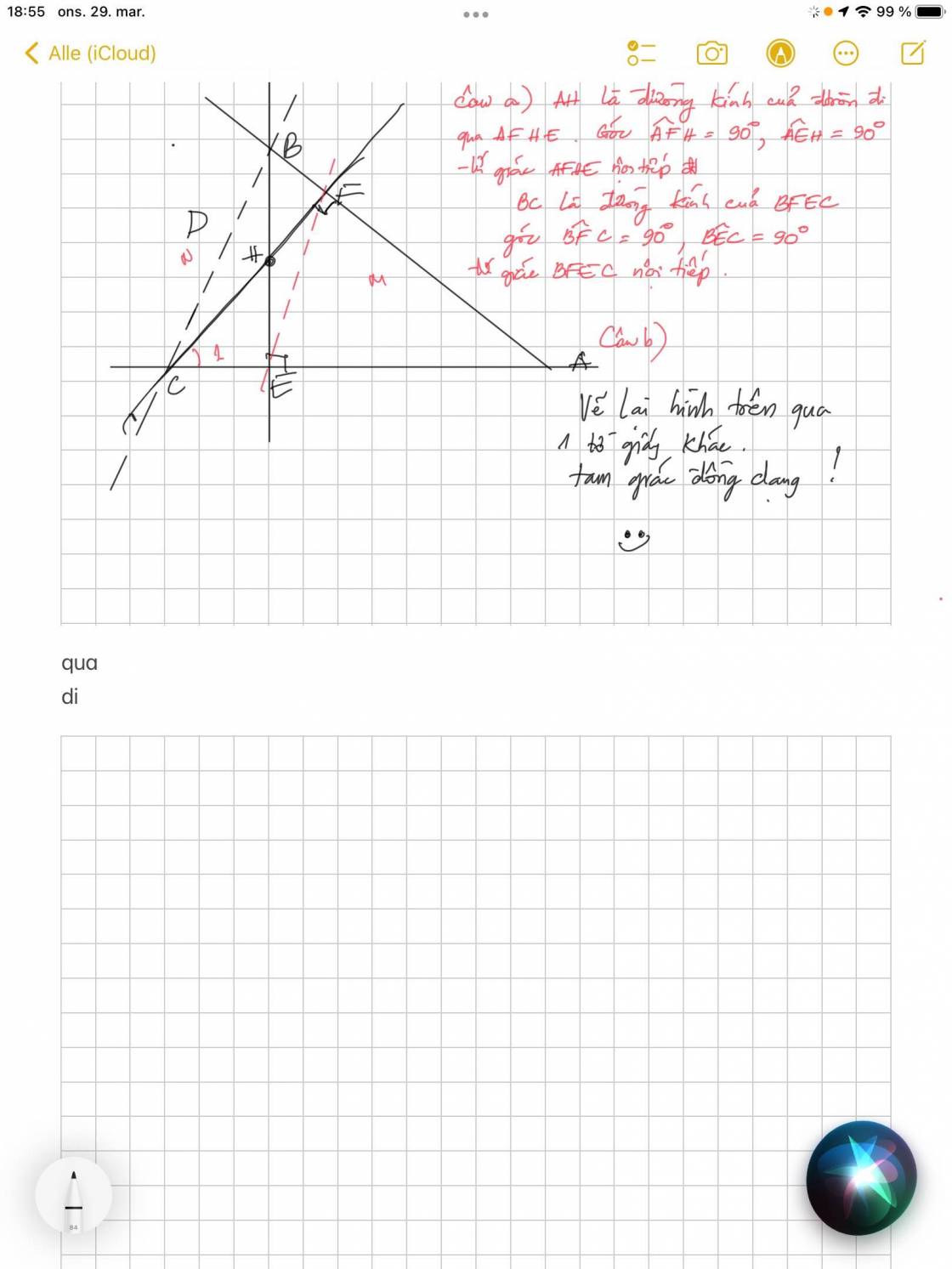
Ta có:

\(4\sqrt{x}=2\sqrt{4x}\le4+x\\ \Rightarrow x^2+4-4\sqrt{x}\ge x^2-x\\ \Rightarrow\sqrt{x^2+4-4\sqrt{x}}\ge\sqrt{x^2-x}\) 

\(6\sqrt{x}=2\sqrt{9x}\le9+x\\ \Rightarrow\sqrt{x^2+4-6\sqrt{x}}\ge\sqrt{x^2-x-5}\)

Suy ra \(1\ge\sqrt{x^2-x}+\sqrt{x^2-x-5}\)

Đặt \(\sqrt{x^2-x}=a;0\le a\le1\\ \sqrt{x^2-x-5}=b;0\le b\le1.\\ \Rightarrow a^2-b^2=\left(x^2-x\right)-\left(x^2-x-5\right)=5.Vôlí\)

Vậy phương trình đã cho vô nghiệm.

Với `x \ne 0,x \ne 1` có:

`A=([x\sqrt{x}]/[\sqrt{x}-1]-[x^2]/[x\sqrt{x}])(1/\sqrt{x}-1)^2`

`A=([x\sqrt{x}]/[\sqrt{x}-1]-x/\sqrt{x})([1-\sqrt{x}]/\sqrt{x})^2`

`A=[x^2-x(\sqrt{x}-1)]/[\sqrt{x}(\sqrt{x}-1)].[(\sqrt{x}-1)^2]/x`

`A=[x(x-\sqrt{x}-1)]/\sqrt{x}.[\sqrt{x}-1]/x`

`A=[x-\sqrt{x}-1]/[\sqrt{x}-1]`

ĐKXĐ : 

\(\left\{{}\begin{matrix}\sqrt{a}+2\ne0\\\sqrt{a}-2\ne0\\\sqrt{a}\ne0\\\sqrt{a}x\text{đ}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{a}\ne2\\a\ne0\\a\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a\ne4\\a>0\end{matrix}\right.\)

Rút gọn :

\(\left(\dfrac{\sqrt{a}-2}{\sqrt{a}+2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-2}\right).\left(\sqrt{a}-\dfrac{4}{\sqrt{a}}\right)\)

\(=\dfrac{\left(\sqrt{a}-2\right)^2-\left(\sqrt{a}+2\right)^2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}.\dfrac{a-4}{\sqrt{a}}\)

\(=\dfrac{\left(\sqrt{a}-2+\sqrt{a}+2\right)\left(\sqrt{a}-2-\sqrt{a}-2\right)}{\left(\sqrt{a}\right)^2-2^2}.\dfrac{a-4}{\sqrt{a}}\)

\(=\dfrac{2\sqrt{a}.\left(-4\right)}{\sqrt{a}}\)

\(=2.\left(-4\right)=-8\)

ta có \(\sqrt{\left(a+c\right)\left(a+b\right)}\ge a+\sqrt{bc}\left(1\right)\)

thật vậy \(\left(1\right)\Leftrightarrow\left(a+c\right)\left(a+b\right)\ge a^2+2a\sqrt{bc}+bc\)

\(\Leftrightarrow ab+ac\ge2a\sqrt{bc}\Leftrightarrow b+c\ge2\sqrt{bc}\)(đúng theo BĐT cosi)

cminh tương tự \(\Rightarrow\sqrt{\left(b+c\right)\left(b+a\right)}\ge b+\sqrt{ac};\sqrt{\left(c+a\right)\left(c+b\right)}\ge c+\sqrt{ab}\)

\(\Rightarrow\dfrac{a}{\sqrt{\left(a+c\right)\left(a+b\right)}}\le\dfrac{a}{a+\sqrt{bc}}=\dfrac{1}{1+\dfrac{\sqrt{bc}}{a}}\)

\(tt\Rightarrow P\le\dfrac{1}{1+\dfrac{\sqrt{bc}}{a}}+\dfrac{1}{1+\dfrac{\sqrt{ac}}{b}}+\dfrac{1}{1+\dfrac{\sqrt{ab}}{c}}\)

\(đặt\left(\dfrac{\sqrt{bc}}{a};\dfrac{\sqrt{ac}}{b};\dfrac{\sqrt{ab}}{c}\right)=\left(x;y;z\right)\Rightarrow xyz=1\)

\(\Rightarrow P\le\dfrac{1}{x+1}+\dfrac{1}{y+1}+\dfrac{1}{z+1}\)

ta đi chứng minh \(\dfrac{1}{x+1}+\dfrac{1}{y+1}+\dfrac{1}{z+1}\le\dfrac{3}{2}\)

\(\Leftrightarrow2\left(y+1\right)\left(z+1\right)+2\left(x+1\right)\left(z+1\right)+2\left(x+1\right)\left(y+1\right)\le3\left(x+1\right)\left(y+1\right)\left(z+1\right)\)

\(\Leftrightarrow2xy+2xz+2yz+4x+4y+4z+6\le3xyz+3+3xy+3xz+3yz+3x+3y+3z\)

ủa đến đây theo cách làm bth đúng rồi mà sao không ra nhỉ bạn xem lại hộ mình giống bài  n ày mình từng làm r

https://hoc24.vn/vip/289470733648/page-12

Toán 9

I'm don't know

14 balls are not blue.    => yellow + red + pink = 14
16 balls are not yellow. => blue + red + pink = 16
24 balls are not red.      => blue + yellow + pink = 24
12 balls are not pink.    => blue + yellow + red = 12

====> 3 yellow + 3 red + 3 blue + 3 pink = 14+16+24+12
    3(yellow + red + blue + pink) = 66
    yellow + red + blue + pink = 66:3 =22