[GIỚI THIỆU VỀ FORM KHẢO SÁT KHOA HỌC - BUỔI TƯƠNG TÁC TRỰC TIẾP SỐ 1, NĂM 2025]
Đường link: https://olm.vn/s/khaosatOLMHoc24
Thể lệ chi tiết: https://olm.vn/s/khaosatOLMthele
Trong những ngày đầu năm mới, Hoc24 và OLM đặt mục tiêu năm 2025 sẽ là năm tập trung hoàn toàn đến cải tiến trải nghiệm sử dụng các sản phẩm, các trang web của người dùng. Chính vì vậy, đội ngũ nghiên cứu đến từ Hoc24 và OLM, và Đại học Kinh tế Quốc dân đã xuất bản phiếu khảo sát nghiên cứu về sự thỏa mãn của người dùng khi sử dụng các nền tảng học tập trực tuyến. Ngay bây giờ, bạn cũng có thể đóng góp vào công cuộc phát triển sản phẩm và nền tảng Hoc24 và OLM đấy! 🤩
Rất đơn giản, bạn chỉ cần truy cập vào đường dẫn sau đây: https://olm.vn/s/khaosatOLMHoc24
Trong form khảo sát này, bạn sẽ được hỏi 18 câu hỏi liên quan đến trải nghiệm của bạn trên trang web. Thời gian trả lời khảo sát dự kiến là 3 đến 7 phút, vậy nên hãy dành ra chút thời gian để hỗ trợ đội ngũ nghiên cứu cải tiến các dịch vụ của mình, góp phần giúp bạn có một trải nghiệm toàn vẹn hơn nhé! 🥰
Ngay sau khi các bạn điền form thành công, BTC sẽ gửi tới các bạn 5 COIN (5.000đ) và 10GP sớm nhất có thể! Ngoài ra, với mỗi bạn điền form thành công, hoặc mời bạn bè, các bạn sẽ nhận được 1 mã giảm giá các dịch vụ của OLM lên đến 10% đó! 🥳
Một điểm mới được công bố, đó chính là sự trở lại của nhiệm vụ "Mời bạn bè - nhận thưởng khủng" đó! Với mỗi 100 người bạn mời điền thành công, bạn sẽ được BTC chuyển thưởng ngay 25.000đ tiền thưởng đó! Một điểm khác biệt là khoản thưởng này sẽ được chuyển sau khi kết thúc đợt khảo sát, và BTC sẽ theo dõi và thông báo đến các bạn thường xuyên mức thưởng của các bạn! 😍
ℹ Ngoài ra, BTC sẽ giới thiệu thêm một số phần thưởng trong hoạt động khảo sát nữa nhé:
a) 1 vé tham gia bốc thăm trúng thưởng trong chương trình Livestream diễn ra dự kiến vào giữa tháng 4/2025. [MỚI!] Khi mời bạn, người mời và người điền đều nhận được 1 vé.
Cơ cấu giải thưởng:
1 GIẢI NHẤT: 600.000đ.
1 GIẢI NHÌ: 300.000đ.
2 GIẢI BA: 150.000đ.
4 GIẢI TƯ: 80.000đ.
10 GIẢI NĂM: 40.000đ.
20 GIẢI KHUYẾN KHÍCH: 20.000đ.
Lưu ý, quỹ thưởng này có thể thay đổi khi chương trình "Mời bạn bè - nhận thưởng khủng" được triển khai.
b) 10 người mời được nhiều bạn điền form nhất sẽ được nhận phần thưởng tiền mặt đến từ nhà tài trợ OLM và Hoc24.
1 GIẢI NHẤT: 600.000đ.
1 GIẢI NHÌ: 300.000đ.
1 GIẢI BA: 150.000đ.
2 GIẢI TƯ: 100.000đ.
5 GIẢI NĂM: 50.000đ.
c) 50 người mời được nhiều bạn điền form nhất (tối thiểu 5 bạn) sẽ được nhận giấy chứng nhận có dấu đỏ đến từ Công ty cổ phần Công nghệ Giáo dục Việt Nam.
Một số lưu ý mới khi mời bạn bè điền:
- BTC khuyến khích bạn mời các bạn đến từ thành thị, có giới tính là nam điền, và đến từ những khối lớp ngoài lớp 5 và lớp 7. Điều này là do hiện nay trong form điền đang có khá nhiều bạn nữ điền, và đa số các bạn điền đến từ nông thôn. Tuy nhiên, tất cả mọi người vẫn có thể hỗ trợ BTC bằng cách điền form và mời bạn bè điền, không có bất cứ giới hạn nào!
- Những form điền "không muốn nêu cụ thể" trong mục giới tính và khu vực, BTC sẽ không tính vào form mời thành công từ những bạn mời bạn bè.
Hướng đến mục tiêu một trang web toàn diện và vì nền giáo dục Việt Nam, rất mong các bạn sẽ giúp Hoc24 và OLM đạt được mục tiêu và sứ mệnh cao cả này! 🎉🎉🎉
----------------------------
THÔNG TIN LIÊN HỆ:
- Fanpage: https://www.facebook.com/hoc24.vn
- Email: vemc.contest@gmail.com
- Hotline: 0962 489 785 (Trưởng BTC - GV. Hà Quang Minh)




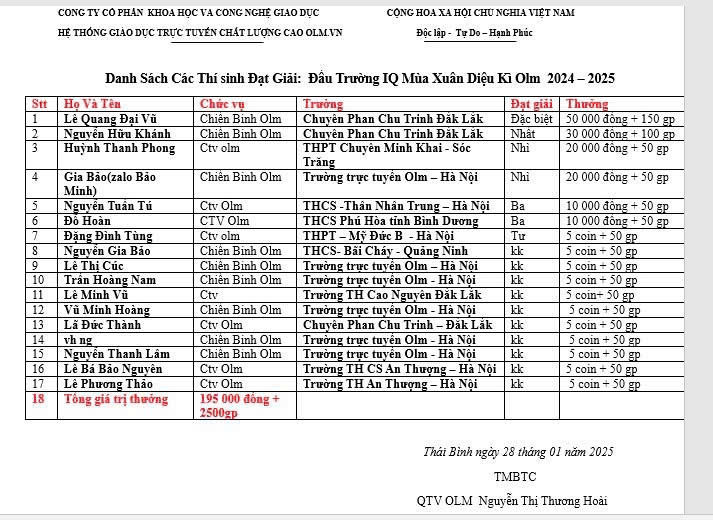
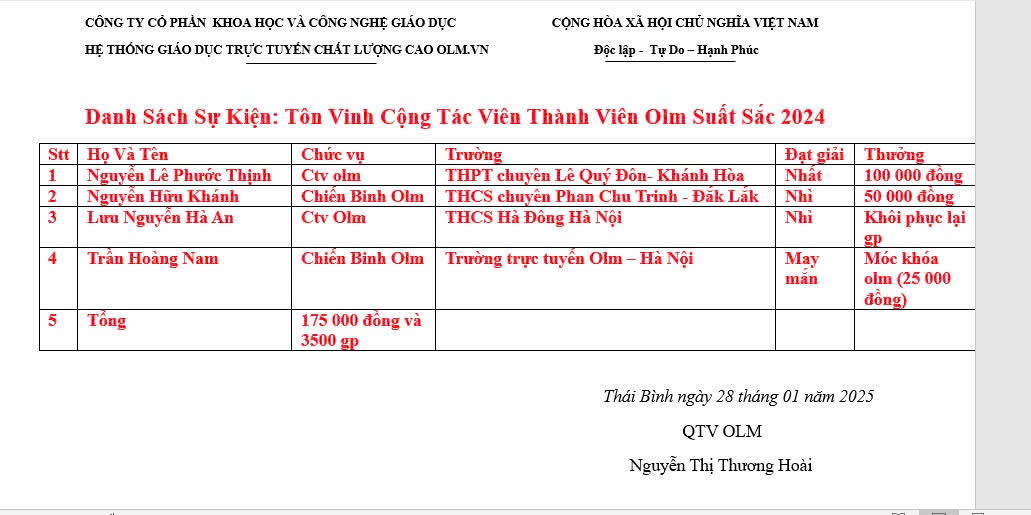
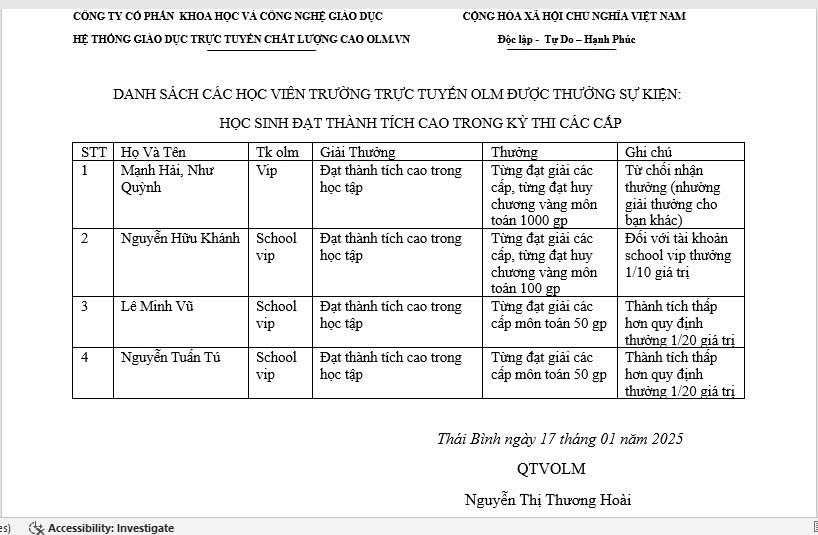
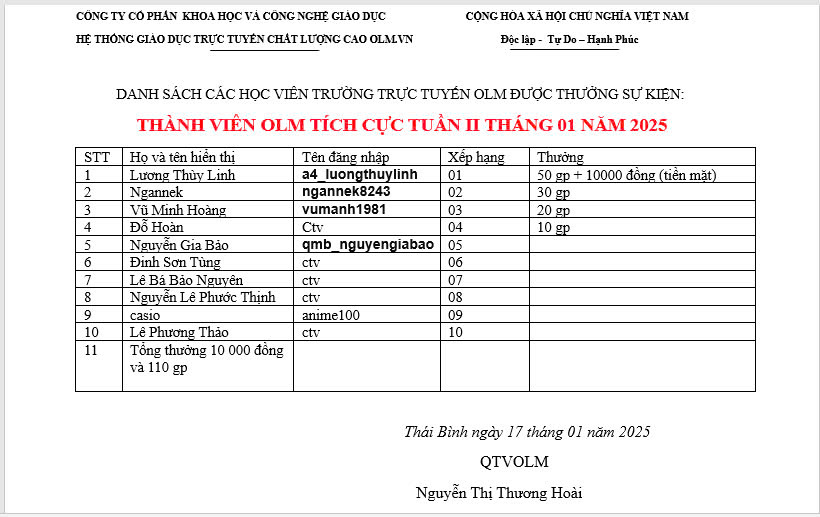

tham gia ngay nek mọi người ơi
wow