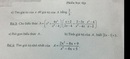Bài làm

Bài 3

a) \(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x+2}{2x-4}+\frac{2-3x}{x^3-4x}\cdot\frac{x^2-4}{x-2}\right)\)

\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x+2}{2\left(x-2\right)}+\frac{2-3x}{x\left(x^2-4\right)}\cdot\frac{x^2-4}{x-2}\right)\)

\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x+2}{2\left(x-2\right)}+\frac{2-3x}{x\left(x-2\right)}\right)\)

\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x\left(x+2\right)}{2x\left(x-2\right)}+\frac{2\left(2-3x\right)}{2x\left(x-2\right)}\right)\)

\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\frac{x^2+2x+4-6x}{2x\left(x-2\right)}\)

\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\frac{x^2-4x+4}{2x\left(x-2\right)}\)

\(A=\left(\frac{x^4-4x^2}{x^2-4}+\frac{4x^2}{x^2-4}\right)\cdot\frac{\left(x-2\right)^2}{2x\left(x-2\right)}\)

\(A=\frac{x^4}{\left(x-2\right)\left(x+2\right)}\cdot\frac{x-2}{2x}\)

\(A=\frac{x^3}{2\left(x+2\right)}\)

Vậy \(A=\frac{x^3}{2\left(x+2\right)}\)

b) Ta có: \(\left|2x-1\right|=3\)

<=> \(\orbr{\begin{cases}2x-1=3\\2x-1=-3\end{cases}}\)<=> \(\orbr{\begin{cases}2x=4\\2x=-2\end{cases}}\)<=> \(\orbr{\begin{cases}x=2\\x=-1\end{cases}}\)

*) Với x = 2 thì ta thay x = 2 vào A ta được:

\(A=\frac{2^3}{2\left(2+2\right)}=\frac{8}{8}=1\)

Vậy với x = 2 thì A = 1

*) Với x = -1 thì ta thay x = -2 vào ta, ta được:

\(A=\frac{\left(-1\right)^3}{2\left(-1+2\right)}=\frac{-1}{2}\)

Vậy với x = -1 thì x = -1/2

Bài 2:

a) \(A=\left(\frac{x+2}{x^2+2x+1}-\frac{x-2}{x^2-1}\right):\frac{2x^2+x}{x^3+x^2-x-1}\)

\(A=\left(\frac{x+2}{\left(x+1\right)\left(x+1\right)}-\frac{x-2}{\left(x+1\right)\left(x-1\right)}\right):\frac{2x^2+x}{x^2\left(x+1\right)-\left(x+1\right)}\)

\(A=\left(\frac{\left(x+2\right)\left(x-1\right)}{\left(x+1\right)\left(x+1\right)\left(x-1\right)}-\frac{\left(x-2\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)\left(x+1\right)}\right):\frac{2x^2+x}{\left(x+1\right)\left(x+1\right)\left(x-1\right)}\)

\(A=\left(\frac{x^2+2x-x-2}{\left(x+1\right)^2\left(x-1\right)}-\frac{x^2+x-2x-2}{\left(x+1\right)^2\left(x-1\right)}\right)\cdot\frac{\left(x+1\right)^2\left(x-1\right)}{x\left(2x+1\right)}\)

\(A=\frac{x^2+2x-x-2-x^2-x+2x+2}{\left(x+1\right)^2\left(x-1\right)}\cdot\frac{\left(x+1\right)^2\left(x-1\right)}{x\left(2x+1\right)}\)

\(A=4x-2x\cdot\frac{1}{x\left(2x+1\right)}\)

\(A=\frac{2x\left(2-1\right)}{x\left(2x+1\right)}\)

\(A=\frac{4-2}{2x+1}\)

\(A=\frac{2}{2x+1}\)

Để A xác định

<=> 2x + 1 khác 0

<=> 2x khác -1

<=> x khác -1/2

Vậy x khác -1/2 thì A xác định.

b) Thay x = -3 vào A ta được:

\(A=\frac{2}{2\left(-3\right)+1}=\frac{2}{-6+1}=\frac{2}{-5}\)

Vậy x = -3 thì A = 2/-5

Thay x = 1/4 vào A ta được

\(A=\frac{2}{2\cdot\frac{1}{4}+1}=\frac{2}{\frac{1}{2}+1}=\frac{2}{\frac{3}{2}}=2:\frac{3}{2}=2\cdot\frac{2}{3}=\frac{4}{3}\)

Vậy x = 1/4 thì A = 4/3

Vì x = -1/2 (Không thỏa mãn điều kiện)

Do đó với x = -1/2 thì A không xác định.

c) Để |A| = 3

<=> \(\left|\frac{2}{2x+1}\right|=3\)

<=> \(\orbr{\begin{cases}\frac{2}{2x+1}=3\\\frac{2}{2x+1}=-3\end{cases}\Leftrightarrow\orbr{\begin{cases}6x+3=2\\-6x-3=2\end{cases}\Leftrightarrow}\orbr{\begin{cases}6x=-1\\-6x=5\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-\frac{1}{6}\\x=-\frac{5}{6}\end{cases}}}\)

Vậy x = -1/6 hoặc x = -5/6 thì |A| = 3

\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\left(\frac{x+2}{2x-4}+\frac{2-3x}{x^3-4}.\frac{x^2-4}{x-2}\right)\)

\(=\left(\frac{x^2\left(x^2-4\right)}{x^2-4}+\frac{4x^2}{x^2-4}\right)\left(\frac{x+2}{2\left(x-2\right)}+\frac{\left(2-3x\right)\left(x^2-4\right)}{x\left(x^2-4\right)\left(x-2\right)}\right)\)

\(=\left(\frac{x^2\left(x^2-4\right)+4x^2}{x^2-4}\right)\left(\frac{x+2}{2\left(x-2\right)}+\frac{2-3x}{x\left(x-2\right)}\right)\)

\(=\left(\frac{x^4-4x^2+4x^2}{x^2-4}\right)\left(\frac{x\left(x+2\right)}{2x\left(x-2\right)}+\frac{2\left(2-3x\right)}{2x\left(x-2\right)}\right)\)

\(=\left(\frac{x^4}{x^2-4}\right)\left(\frac{x^2+2x+4-6x}{2x\left(x-2\right)}\right)=\left(\frac{x^4}{x^2-4}\right)\left(\frac{x^2-4x+4}{2x\left(x-2\right)}\right)\)

\(=\left(\frac{x^4}{x^2-4}\right)\left(\frac{\left(x-2\right)^2}{2x\left(x-2\right)}\right)=\left(\frac{x^4}{x^2-4}\right)\left(\frac{x-2}{2x}\right)=\frac{x^4.\left(x-2\right)}{\left(x^2-4\right)2x}\)

\(=\frac{x^4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)2x}=\frac{x^3}{2\left(x+2\right)}\)

b,Ta có:\(\left|2x-1\right|=3\)

\(\Leftrightarrow2x-1=\pm3\)

\(\Leftrightarrow\orbr{\begin{cases}2x-1=3\\2x-1=-3\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}}\)

Với x=2 thì giá trị của A là:\(\frac{2^3}{2\left(2+2\right)}=1\)

Với x=-1 thì giá trị biểu thức là:\(\frac{\left(-1\right)^3}{-2\left(-1+2\right)}=-\frac{1}{2}\)

2x³-6x²

=2x².(x-3)

# hok tốt#

Kẻ \(AH\perp DC\) , \(BK\perp DC\)

Xét tứ giác ABKH có: AB // HK (gt)

                                   AH // BK ( cùng \(\perp DC\))

=> ABKH là hình chữ nhật (dhnb)

=> HK = AB = 4, AH = BK

Xét △ ADH vuông tại H và △BCK vuông tại K

Có: AH = BK (cmt)

      AD = BC (ABCD là hình thang cân)

=> △ADH = △BCK (ch-cgv)

=> DH = KC

Ta có: DH + HK + KC = DC

=> 2DH + HK = 10

=> 2DH + 4 = 10

=> 2DH = 6

=> DH = 3 = CK

Ta có: DK = DH + HK = 3 + 4 = 7

Xét △DEF vuông tại F có: BF là đường trung tuyến

=> BF = BD = DE/2

=> △BFD cân tại B

mà BK là đường cao ( \(BK\perp DF\))

=> BK là đường trung tuyến

=> DK = KF = 7

Ta có: CF = KF - KC = 7 - 3 = 4

Xét tức giác AKBH có :

AD = DB ( do D là trung điểm AB )
KD = DH ( do H đối xứng với K qua D)
=> AHBK  là hình bình hành 
Mà \(\widehat{AHB}=90^0\)
=> AHBK là hình chữ nhật ( đpcm )

b) 
Do \(DE//BC\)
\(\Rightarrow DE//HF\)
=> DEFH là hình thang ( 1 )
Do AKBH là hình chữ nhật 
\(\Rightarrow AB=KH\)
\(\Rightarrow\frac{1}{2}AB=\frac{1}{2}KH\)
\(\Rightarrow BD=DH\)
Mà EF = BD ( do EF  là đường trung bình ) 
=> DH = EF (2)
Từ (1) và (2) suy ra DEFH là hình thang cân 
 

\(a)\)\(x^2-y^2-2x+2y\)

\(=\left(x^2-2x+1\right)-\left(y^2-2y+1\right)\)

\(=\left(x-1\right)^2-\left(y-1\right)^2\)

\(=\left(x-y\right)\left(x+y-2\right)\)

\(b)\)\(x^2+4y^2-25+4xy\)

\(=\left(x^2+4xy+4y^2\right)-25\)

\(=\left(x+2y\right)^2-25\)

\(=\left(x+2y-5\right)\left(x+2y+5\right)\)

Dumflinz

sai đề r nha bạn, làm j có điểm D

thế mà cũng đòi viết học ngu