Sự đồng quy của ba đường trung tuyến, ba đường phân giác của tam giác SVIP

1. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN TRONG MỘT TAM GIÁC

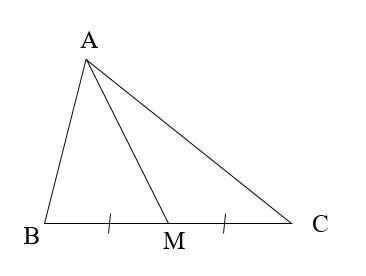
Đường trung tuyến của tam giác

Đoạn thẳng \(AM\) nối đỉnh \(A\) của tam giác \(ABC\) với trung điểm \(M\) của cạnh \(BC\) gọi là đường trung tuyến (xuất hát từ đỉnh \(A\) hoặc ứng với cạnh \(BC\)) của tam giác \(ABC\) 

Sự đồng quy của ba đường trung tuyến

Định lý 1. Ba đường trung tuyến của một tam giác cùng đi qua một điềm (hay đồng quy tại một điểm). Điểm đó cách mỗi đỉnh một khoảng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.

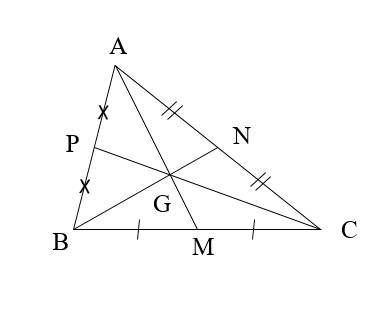
Ví dụ. Trong tam giác \(ABC\), các đường trung tuyến \(AM,BN,CP\) đồng quy tại \(G\) và \(AG=\dfrac{2}{3}AM;BG=\dfrac{2}{3}BN;CG=\dfrac{2}{3}CP.\)

2. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG PHÂN GIÁC TRONG TAM GIÁC

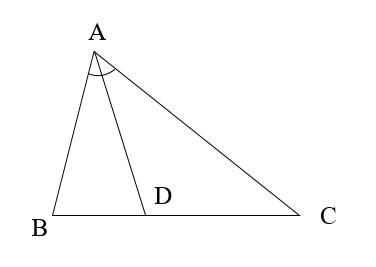
Đường phân giác của tam giác

Trong tam giác \(ABC\), tia phân giác của góc \(A\) cắt cạnh \(BC\) tại điểm \(D\) thì đoạn thẳng \(AD\) được gọi là đường phân giác (xuất phát từ đỉnh \(A\)) của tam giác \(ABC\).

Sự đồng quy của ba đường phân giác

Định lý 2. Ba đường phân giác của tam giác đồng quy tại một điểm. Điểm này cách đều ba cạn của tam giác đó.

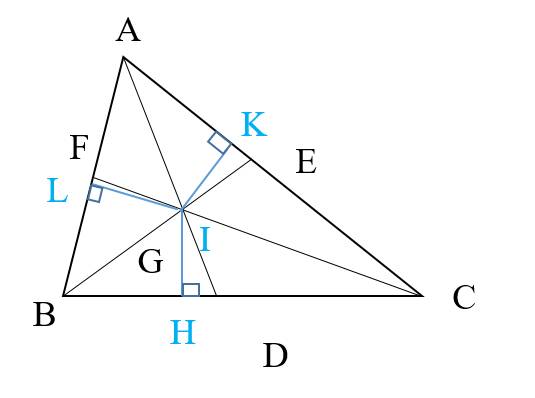
Ví dụ. Trong tam giác \(ABC\), các đường phân giác \(AD,BE,CF\) đồng quy tại \(I\) và \(\text{IH = IK = IL.}\)