Bài học cùng chủ đề
- Sự đồng quy của ba đường trung tuyến trong tam giác
- Sự đồng quy của ba đường phân giác trong tam giác
- Đường trung tuyến của tam giác
- Tính chất ba đường trung tuyến của tam giác
- Đường phân giác của tam giác
- Tính chất ba đường phân giác của tam giác
- Tính chất ba đường trung tuyến trong tam giác
- Bài tập tự luận: sự đồng quy của ba đường trung tuyến
- Tính chất ba đường phân giác trong tam giác
- Bài tập tự luận: sự đồng quy của ba đường phân giác của tam giác
- Phiếu học tập: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tính chất ba đường trung tuyến trong tam giác SVIP
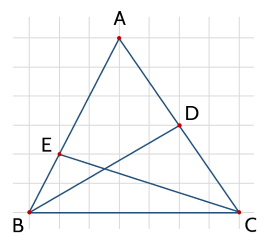
Đoạn thẳng nào dưới đây là đường trung tuyến của tam giác ABC?
Trong hình vẽ trên, đoạn thẳng AM là đường trung tuyến của những tam giác nào?
Dựa vào hình vẽ, điền số thích hợp vào ô trống.
FBFG= ; FBGB= ;
AGAM= ; GMAM= .
(Kéo thả hoặc click vào để điền)
Tam giác ABC có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Khi đó
Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD=BA. Trên cạnh BC lấy điểm E sao cho BE=31BC. Gọi K là giao điểm của AE và CD.
Sắp xếp các dòng sau một cách hợp lí để hoàn thiện chứng minh CK=KD.
- Điểm E thuộc đoạn CB và CE=32CB nên E là trọng tâm của ΔACD.
- Xét ΔACD, ta có CB là đường trung tuyến.
- Do đó, AK là đường trung tuyến của ΔACD, vậy CK=KD.
Tam giác ABC có hai đường trung tuyến BD, CE bằng nhau. Chứng minh tam giác đó là tam giác cân.
Sắp xếp các dòng sau một cách hợp lí để hoàn thành lời giải:
- Gọi G là giao điểm của BD và CE.
- Vậy ΔABC là tam giác cân.
- Do đó ΔBGE=ΔCGD (c.g.c), suy ra BE=CD.
- Mà BE=21AB; CD=21AC nên AB=AC.
- Ta có: EG=31CE; DG=31BD⇒EG=DG.
và CG=32CE; BG=32BD⇒CG=BG.
Tam giác ABC có BC=10 cm, các đường trung tuyến BD và CE.
Sắp xếp các dòng sau một cách hợp lí để hoàn thành chứng minh rằng BD+CE>15 cm.
- Gọi G là giao điểm của BD và CE. Theo bất đẳng thức trong tam giác GBC:
- BD+CE>23.10 cm =15 cm.
- GB+GC>BC=10 cm.
- 32BD+32CE>10 cm.
Tam giác ABC có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Gọi E và F lần lượt là trung điểm của BD và BG.
Điền số thích hợp vào ô trống:
BC= . BM;
AB= . GE;
AC= . DF.

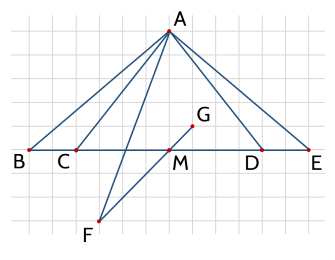
Quan sát hình vẽ và hoàn thành các khẳng định sau:
a) Đoạn thẳng BN là đường trung tuyến của tam giác .
b) Đoạn thẳng AD là đường trung tuyến của tam giác và tam giác B.
c) Đoạn thẳng là đường trung tuyến của tam giác EAD.
d) Điểm là trọng tâm của tam giác ABC.
(Kéo thả hoặc click vào để điền)

Cho tam giác ABC có trung tuyến BM và CN cắt nhau tại G. Biết BG = 4 cm, CN = 9 cm. Tính độ dài của các đoạn thẳng BM và GN.
Đáp án: BM = cm; GN = cm.

Bạn có thể đăng câu hỏi về bài học này ở đây
