Bài học cùng chủ đề
- Định lí côsin và định lí sin
- Định lý côsin
- Định lí sin
- Một số công thức tính diện tích tam giác
- Giải tam giác
- Giải tam giác
- Giải tam giác (Nâng cao)
- Ứng dụng giải tam giác vào thực tế
- Bán kính đường tròn ngoại tiếp và nội tiếp trong tam giác
- Diện tích tam giác
- Phiếu bài tập: Hệ thức lượng trong tam giác
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Định lý côsin SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Định lí côsin
Trong tam giác $A B C$ :
$a^2=b^2+c^2-2 b c \cos A$,
$b^2=c^2+a^2-2 c a \cos B$,
$c^2=a^2+b^2-2 a b \cos C$.
$a^2=b^2+c^2-2 b c \cos A$,
$b^2=c^2+a^2-2 c a \cos B$,
$c^2=a^2+b^2-2 a b \cos C$.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
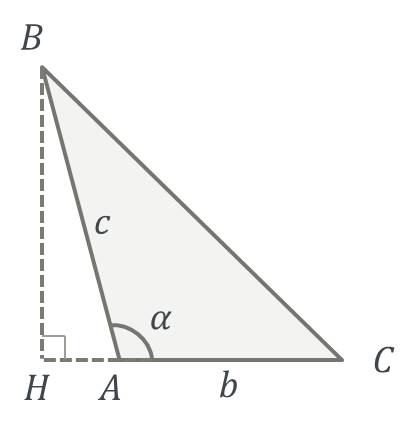
BH2= .
CH2= .
AB2+AH2 (CA−AH)2(CA+AH)2 AB2−AH2
(Kéo thả hoặc click vào để điền)
Câu 2 (1đ):

BAH= ;
cosBAH= .
cosα α−cosα 180∘−α
(Kéo thả hoặc click vào để điền)
Câu 3 (1đ):
Điền biểu thức thích hợp vào ô trống.
a2=b2+c2−2bc.cosA⇒cosA= .
2abb2+c2−a22bcb2+c2−a2
(Kéo thả hoặc click vào để điền)
Câu 4 (1đ):
Trong tam giác ABC, BC=
A
AB2+AC2−2AB.AC.cosC.
B
AB2+AC2−2AB.AC.cosB.
C
AB2+AC2−2AB.AC.cosA.
Câu 5 (1đ):
cosB=71 thì B≈ .
8∘12′81∘47′
(Kéo thả hoặc click vào để điền)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- về việc tìm ra các yếu tố trong một tam
- giác bất kì là một công việc rất là quan
- trọng trong đó Đảng nói riêng cũng như
- trong khoảng Nói chung thì Bài học này
- chúng ta sẽ tìm hiểu các định lý các
- công cụ mới có tính ứng dụng một cách
- tổng quát hơn đầu tiên chúng ta sẽ tìm
- hiểu về định lý cosin trong tam giác
- từ trước khi tìm hiểu nội dung ý nghĩa
- câu xin thì chúng ta cùng nhắc lại về
- mối liên hệ trong 3 cạnh mở ra vuông hãy
- chúng ta còn gọi nó là định lý Pitago
- thì cho tam giác vuông ABC thì cạnh
- huyền a sẽ bằng gì nó sẽ bằng
- căn bậc hai tổng bình phương của hai
- cạnh góc vuông hay với cách khác Chúng
- tôi biết là A Bình Phương sẽ bằng b bình
- phương + c Bình Phương đi Phước Thịnh
- huyền bằng tổng bình phương các vị vua
- Đây là công cụ rất hiệu để tính ra các
- cạnh của giác vuông
- Một Câu hỏi đặt ra là một tam giác bất
- kì sao
- anh ở đây lịch ví dụ cho trường
- cho tam giác tù
- khi chúng ta có một định lý nào mà tương
- tự như định lý Pitago không Tức là gì ta
- biết được hai cạnh
- A và ta biết được góc xen giữa của đó
- thì ta có tìm được cạnh còn lại không
- Câu trả lời là có đó chính là định lý
- cosin và ra thì học về sau đây cái cảm
- thời chúng ta quên cái tên định lí cosin
- đi
- khi chúng ta cũng giải bài toán là trong
- tam giác ABC đã biết cạnh AC = B biết
- cạnh AB = c biết góc xen giữa của cạnh
- AB và AC là pha sẽ tính cạnh BC là cạnh
- a Theo B điểm C và ta như thế nào đây là
- bài toán không hề phức tạp một chút nào
- chúng ta có các công cụ đã học đó là ý
- vì đã nho mối liên hệ giữa cạnh và góc
- trong tam giác trong tam giác vuông thì
- bây giờ để áp dụng được các công cụ đó
- thì ta phải tạo ra do vuông thì phải sẽ
- tạo ra từ nó vô mấy cái kiểu gì thấy xe
- hạng vuông góc từ B dự định là D
- bài hát gì ở đây thì đã tạo ra cho nó
- vuông bhc thấy góc vuông ở đây nhằm mục
- đích là gì ta sẽ tạo là thằng vuông có
- cạnh huyền là ah chính là một cạnh mà ta
- đang thấy thì bây giờ ta sẽ xem a Tính
- theo các cạnh của tam giác obc là như
- thế nào để thuận tiện thì thầy sẽ sử
- dụng bình phương thì ta có là gì theo
- định lý Pitago Bình Phương sẽ bằng
- ph Bình + ch Bình ph bình phương
- ta sẽ biết nó thành biểu thức nào
- a ph bình phương ta thấy nó nằm trong
- tam giác vuông b DHA có cạnh huyền là C
- tin tức là nó bảng A b bình phương - 22
- bình phương ở tạm thời ta cứ để như vậy
- a ch bình phương thì sao
- Anh ta sẽ biến đổi ch theo cạnh Satan là
- cạnh b đã biết thì nó sẽ = AC + a bình
- phương
- ê ê Ace + axit ở địa phương như vậy thì
- thế vào đây ta sẽ được là gì A Bình sẽ =
- a b bình chứa bình cộng với a bình
- phương cộng 2 lần AC + Vectơ cùng phương
- thì
- đây ta sẽ rút gọn giảm lượng được các
- bình phương a b bình cộng c bình cộng
- hai lần hnc
- A AB đó chính là C bình phương rồi AC nó
- là b bình phương người ta cần xử lý hát
- này
- chị đã đưa về B và C
- a và giá trị lượng giác của gọi pha thế
- thì ai hát ta thấy nó nằm trong tam giác
- vuông bê tha như vậy thì ah nó sẽ bằng
- cosin của góc B Cái này nó có liên hệ gì
- với cosin của góc Anpha
- ta thấy góc BH này nó bù với con ta thế
- cho nên là nó sẽ bằng đối
- Côsi của nó sẽ bằng đối kushi của các
- bang như vậy ta sẽ biết là chữ AB nhân
- với cosin của góc Anpha
- mà thay vào đây là có cái quả là bằng a
- b bình phương cộng a bình phương cộng 2
- lần ab nhân với cosin
- ý của 180 độ truyền Alpha trên pc và ta
- rút gọn lại ta được kết quả là b bình
- cộng c Bình - 2 lần BC cosin góc A1
- chính là gọi Alpha
- như vậy thì phóng hoàn lại Nếu một tam
- giác ta đã biết được hai cạnh cũng như
- góc xen giữa của cạnh đó thì ta có thể
- tính cá thể còn lại ta có hệ thức là a
- bình phương = b bình cộng c bình trừ 2
- lần BC nhân cos A và ta có thể thấy ngay
- là trong trường hợp đặc biệt góc A là
- góc vuông thì ta có ngay cosin của góc
- vô là thứ bí độ nó bằng không thì ta có
- hệ thức chính nằm định lý Pitago bây giờ
- cái phát biểu hệ thức này bằng lời khi
- phát được một lời chúng ta sẽ ghi nhớ
- được ý thức về hơn
- Ừ thì ta có là trong của tam giác bình
- phương của một cạnh
- chị sẽ bằng tổng bình phương hai cạnh
- kia - 2 lần tích của hai cạnh này nhân
- với cosin góc giữa cạnh đó
- khi mở cài cố gắng phát biểu tưởng tượng
- và phát biểu là một lời nhá
- Anh em chú ý lắng vừa rồi thầy chứng
- minh hệ thức chúng ta gọi là định lý
- cosin trong trường hợp góc chúng ta là
- góc tù trong trường hợp góc nhọn thì em
- có làm tương tự như vậy thì bây giờ dựa
- vào ý thức vừa rồi chúng ta cũng sẽ tính
- được góp dựa vào các cạnh của một tam
- giác bất kì giữ vai thức a bình bằng b
- bình cộng c bình trừ 2 lần BC nhân cos
- của ai thì các em hãy xây dựng giải thức
- tính cosin của em
- tắt có nó bạn bè mình cũng thấy mình
- chưa bình trên 2 PC tương tự code b sẽ
- bằng a bình cộng c bình trừ b bình chỉ
- dài ren A và dựa vào hình thức này ta có
- QC bằng a bình cộng b bình trừ c bình
- trên dây AB một tam giác mà chúng ta
- biết được hai cạnh và góc xen giữa hai
- hình đó tao thể tính được tất cả các Thu
- xuống còn lại về cạnh và góc của tam
- giác đó
- Bây giờ chúng ta sẽ cùng vận dụng vào
- bài làm sau A
- a Cho tam giác ABC có cạnh ab = 5 AC = 8
- góc A bằng 60 độ tính số đo góc B và
- tính chiều dài cạnh BC có cách vận dụng
- định lí cosin và đạt được học để giảm
- thời gian này ở đây người ta cho góc A
- và cạnh AB cạnh AC đi ta thấy góc A này
- nó chính là góc xen giữa của hai cạnh AB
- và sai rồi ta có thể sử dụng được ngay
- đến những cô xin vào đây
- PC Bình Phương nó sẽ phẳng AB bình cộng
- c bình trừ 2 lần tích AB AC nhân vật của
- dãy hoa thì ta chỉ cần thay số vào
- các chú ý cosin của ai tất cả cô sinh 60
- độ là 1/2 thì ta tính được BC = 7
- Ừ để tính số đo góc B thì ta sẽ dựa vào
- ta sẽ tìm cushion của B thích cô single
- bằng gì
- khi cô sinh của BC = b mình BC bình cộng
- b bình trừ ACB trên hai lần tích bc n b
- Ừ thì chúng ta thay số vào ta sẽ có là B
- cosin của B = 17 thì đến nay ta sẽ bật
- máy tính xem B bằng bao nhiêu độ b sẽ
- xấp xỉ và nhiệt độ thời gian nhất và cho
- em cách để chúng ta tìm được số đo của
- góc khi biết được giá trị lượng giác của
- góc đó
- anh ở đây góc của chúng ta luôn ấn độ
- thì cay và chú ý là
- ở chế độ của chúng ta trên máy tính đó
- là chế độ D như thế này nếu mà chưa phải
- thì được b thì cái bấm ship mốt
- A và chọn
- 3D dj&a
- anh ở đây thì cô xin bay bằng 1/7 thì
- thấy sẽ đấm ship có cốt ở đây và thể bấm
- một chia 7 còn một phần 7
- em thấy được kết quả đó là 81 phẩy 786
- thì ta bấm nút
- chế độ này sẽ được cái quả là 81 độ 47
- phút 12,4 giây
- thì ta sẽ biết B xấp xỉ số đó bằng 84 độ
- 47 phút như vậy thì chúng ta đã được tìm
- hiểu xong về định lý Côsi
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
