a) Gọi $(O^{\prime })$ là đường tròn đường kính $OA$.

Vì $O{O}^{\prime }=OA-O^{\prime }A$ nên hai đường tròn $(O)$ và $(O^{\prime })$ tiếp xúc trong.

b) Các tam giác cân $A{O}^{\prime }C$ và $AOD$ có chung góc ở đỉnh $A$ nên $\widehat{AC{O}^{\prime }}=\hat{D}$, suy ra $O^{\prime }C$ // $OD$.

Tam giác $AOD$ có $A{O}^{\prime }=O^{\prime }O$ và $O^{\prime }C$ // $OD$ nên $AC=CD$.

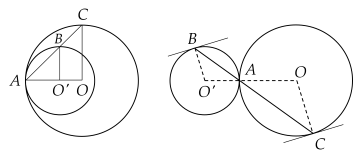
Trường hợp 1: $(O)$ và $(O^{\prime })$ tiếp xúc trong.

Xét $\Delta OAC$, ta có:

$\genfrac{}{}{0ex}{}{O^{\prime }B}{OC}=\genfrac{}{}{0ex}{}{r}{R}=\genfrac{}{}{0ex}{}{O^{\prime }A}{OA}$ suy ra $O^{\prime }B$ // $OC$.

Suy ra các tiếp tuyến tại $B$ và $C$ song song với nhau vì chúng lần lượt vuông góc với $O^{\prime }B$ và $OC$.

Trường hợp 2: $(O)$ và $(O^{\prime })$ tiếp xúc ngoài.

Ta thấy $\Delta O^{\prime }AB\backsim \Delta OAC$ (g.g)

Suy ra $\genfrac{}{}{0ex}{}{O^{\prime }B}{OC}=\genfrac{}{}{0ex}{}{r}{R}=\genfrac{}{}{0ex}{}{O^{\prime }A}{OA}$

Nên $O^{\prime }B$ // $OC$.

Lập luận tương tự như trên, ta được điều phải chứng minh

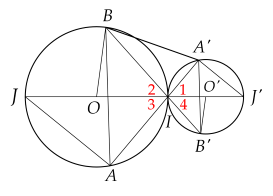
a) Ta có: $O{O}^{\prime }=OI+O^{\prime }I$.

Vậy hai đường tròn tiếp xúc ngoài tại $I$.

b) Xét $\Delta AIJ$ và $\Delta A^{\prime }I{J}^{\prime }$ có:

$\hat{A}=\widehat{A^{\prime }}=90^{\circ }$

$\widehat{I^1}=\widehat{I^2}$ suy ra $\Delta AII\backsim \Delta A^{\prime }I{J}^{\prime }$.

c) $\Delta AIJ\backsim \Delta A^{\prime }I{J}^{\prime }$ (g.g) 

Suy ra $\genfrac{}{}{0ex}{}{IA}{I{A}^{\prime }}=\genfrac{}{}{0ex}{}{IJ}{J{I}^{\prime }}=\genfrac{}{}{0ex}{}{10}{4}=\genfrac{}{}{0ex}{}{5}{2}$ (1) 

$\Delta OIB\backsim \Delta O^{\prime }I{B}^{\prime }$  (g.g) suy ra $OB$ // $O^{\prime }{B}^{\prime }$

Suy ra $\widehat{B^1}=\widehat{B^1}$ suy ra $\genfrac{}{}{0ex}{}{IB}{I{B}^{\prime }}=\genfrac{}{}{0ex}{}{OB}{O^{\prime }{B}^{\prime }}=\genfrac{}{}{0ex}{}{5}{2}$ (2)

 Từ (1) và (2) suy ra $\genfrac{}{}{0ex}{}{IA}{I{A}^{\prime }}=\genfrac{}{}{0ex}{}{IB}{I{B}^{\prime }}=\genfrac{}{}{0ex}{}{5}{2}$; $\widehat{AIB}=\widehat{A^{\prime }IB}$

Nên $\Delta IAB\backsim \Delta I{A}^{\prime }{B}^{\prime }$ (c.g.c).

d) $\Delta IAB\backsim \Delta I{A}^{\prime }{B}^{\prime }$ (c.g.c)

Suy ra $\genfrac{}{}{0ex}{}{AB}{A^{\prime }{B}^{\prime }}=\genfrac{}{}{0ex}{}{IA}{I{A}^{\prime }}=\genfrac{}{}{0ex}{}{5}{2}$;

$\genfrac{}{}{0ex}{}{OA}{O^{\prime }{A}^{\prime }}=\genfrac{}{}{0ex}{}{OB}{O^{\prime }{B}^{\prime }}=\genfrac{}{}{0ex}{}{5}{2}$

Suy ra $\genfrac{}{}{0ex}{}{OA}{O^{\prime }{A}^{\prime }}=\genfrac{}{}{0ex}{}{OB}{O^{\prime }{B}^{\prime }}=\genfrac{}{}{0ex}{}{AB}{A^{\prime }{B}^{\prime }}$ suy ra $\Delta AOB\backsim \Delta A^{\prime }{O}^{\prime }{B}^{\prime }$ (c.c.c).

e) $\Delta AOB\backsim \Delta A^{\prime }{O}^{\prime }{B}^{\prime }$ suy ra $\widehat{OBA}=\widehat{O^{\prime }{B}^{\prime }{A}^{\prime }};\widehat{OBI}=\widehat{O^{\prime }{B}^{\prime }{I}^{\prime }}$

Suy ra $\widehat{ABI}=\widehat{A{B}^{\prime }{I}^{\prime }}$ nên $AB$ // $A^{\prime }{B}^{\prime }$.

Tứ giác $AB{A}^{\prime }{B}^{\prime }$ có hai cạnh đối song song nên nó là hình thang

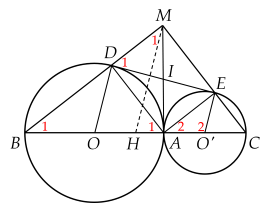
a) Ta có: $\widehat{A^1}=(180^{\circ }-\widehat{O^1}):2$

$\widehat{A^2}=(180^{\circ }-\widehat{O^2}):2$

Suy ra $\widehat{A^1}+\widehat{A^2}=90^{\circ }$ suy ra $\widehat{DAE}=90^{\circ }$.

b) Có tứ giác $ADME$ là hình chữ nhật (tứ giác có ba góc vuông là hình chữ nhật).

c) Gọi $I$ là giao điểm của $DE$ và $AM$ suy ra $ID=IA$

$\Delta IAO=\Delta IDO$ (ccc) suy ra $\widehat{IAO}=\widehat{IDO}=90^{\circ }$

Suy ra $MA\perp OA$ với $A\in (O)$

Chứng minh tương tự: $MA\perp O^{\prime }A$ với $A\in (O^{\prime })$.

Vậy $MA$ là tiếp tuyến chung của hai đường tròn.

 a) Ta có $(2x+1{)}^2-9x^2=0$

$(2x+1-3x)(2x+1+3x)=0$

$(-x+1)(5x+1)=0$

+ Giải phương trình $-x+1=0$

$x=1$

+ Giải phương trình $5x+1=0$

$x=\genfrac{}{}{0ex}{}{-1}{5}$

Vậy phương trình có hai nghiệm là $x=1$ và $x=\genfrac{}{}{0ex}{}{-1}{5}$.

b) Ta có: {5x−4y=32x+y=4{​5x−4y=32x+y=4​

{5x−4y=38x+4y=16{​5x−4y=38x+4y=16​

{13x=192x+y=4{​13x=192x+y=4​

{x=1913y=1413⎩⎨⎧​​x=1319​y=1314​​

Vậy hệ phương trình đã cho có nghiệm $(x;y)=(\genfrac{}{}{0ex}{}{19}{13};\genfrac{}{}{0ex}{}{14}{13})$

Gọi tốc độ của ca nô khi nước yên lặng là $x$ (km/h) ($x>6$ ).

Tốc độ ca nô đi xuôi dòng là $x+6$ (km/h)

Ta có $x\le 40$ nên $x+6\le 40+6$, tức là $x+6\le 46$

Gọi $s$ (km) là quãng đường ca nô đi được trong $2$ giờ $30$ phút $=2,5$ giờ

Ta có $s=2,5.(x+6)$ (km).

Do $x+6\le 46$ nên $2,5.(x+6)<2,5.46$ hay $s\le 115$

Vậy quãng đường ca nô đi được trong $2$ giờ $30$ phút không vượt quá $115$ km.