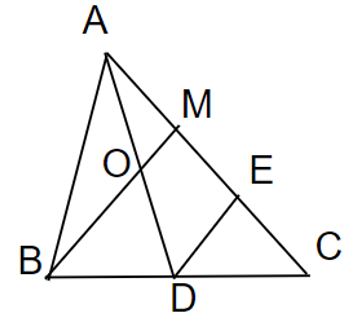
a) Xét Δ ABC có NA = NB; MA = MC

⇒ NM là đường trung bình của ΔABC

⇒ MN // BC;  MN = 1/2 BC   (1)

 Xét Δ GBC có: DG = DB;  EG = EC

⇒ ED  là đường trung bình của Δ GBC

⇒  ED // BC; ED = 1/2 BC

Từ (1) và (2) suy ra: MN // DE;  MN = ED

⇒ Tứ giác NMED là hình bình hành

⇒  ME // ND

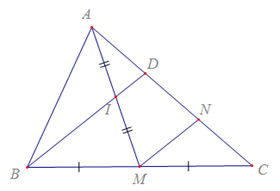
a) Qua M kẻ MN // BD.

Trong $\Delta AMN$, có I là trung điểm của AM, $ID\parallel MN\Rightarrow AD=DN$.

Trong $\Delta BCD$, có M là trung điểm của BC,  $MN\parallel BD\Rightarrow ND=NC$.

$\Rightarrow AD=DN=NC\Rightarrow AD=\frac{1}{2}DC$.

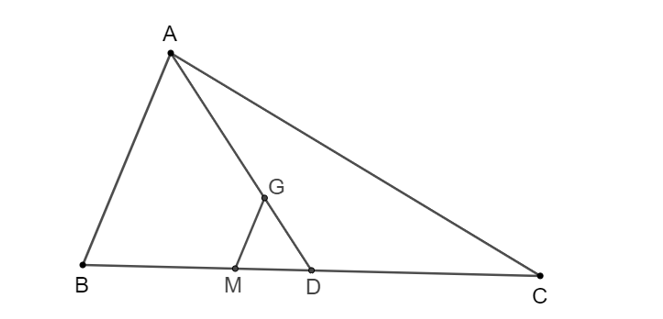
Lấy D là trung điểm của cạnh BC.

Khi đó, AD là đường trung tuyến của tam giác ABC.

Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.

Ta có $\frac{AG}{AD}=\frac{2}{3}$ hay $AG=\frac{2}{3}AD$.

Vì MG // AB, theo định lí Thalès, ta suy ra: $\frac{AG}{AD}=\frac{BM}{BD}=\frac{2}{3}$.

Ta có BD = CD (vì D là trung điểm của cạnh BC) nên $\frac{BM}{BC}=\frac{BM}{2BD}=\frac{2}{2.3}=\frac{1}{3}$.

Do đó $BM=\frac{1}{3}BC$ (đpcm).

Trong ΔADB, ta có: MN // AB (gt)

Suy ra:  hệ quả định lí ta-lét) (1)

Trong ΔACB, ta có: PQ // AB (gt)

Suy ra: 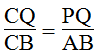 Hệ quá định lí Ta-lét) (2)

Lại có: NQ // AB (gt)

       AB // CD (gt)

Suy ra: NQ // CD

Trong ΔBDC, ta có: NQ // CD (chứng minh trên)

Suy ra: 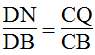(Định lí Ta-lét) (3)

Từ (1), (2) và (3) suy ra 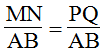 hay MN = PQ

Xét tam giác ABC có BC ⊥ AB' và B'C'⊥ AB' nên suy ra BC // B'C'.

Theo hệ quả định lí Thalès, ta có:

$\frac{AB}{A{B}^{\prime }}=\frac{BC}{B{C}^{\prime }}\Rightarrow \frac{x}{x+h}=\frac{a}{a^{\prime }}\Rightarrow a^{\prime }x=a(x+h)\Rightarrow a^{\prime }x-ax=ah$

$\Rightarrow x\left(a^{\prime }-a\right)=ah\Rightarrow x=\frac{ah}{a^{\prime }-a}$ (đpcm)

Ta có: AB // CD (gt), áp dụng hệ quả của định lý Ta – lét ta có:

Suy ra (hệ quả định lí ta-lét)

Vậy OA.OD = OB.OC