Xét tam giác ABC có BC ⊥ AB' và B'C'⊥ AB' nên suy ra BC // B'C'.

Theo hệ quả định lí Thalès, ta có:

$\frac{AB}{A{B}^{\prime }}=\frac{BC}{B{C}^{\prime }}\Rightarrow \frac{x}{x+h}=\frac{a}{a^{\prime }}\Rightarrow a^{\prime }x=a(x+h)\Rightarrow a^{\prime }x-ax=ah$

$\Rightarrow x\left(a^{\prime }-a\right)=ah\Rightarrow x=\frac{ah}{a^{\prime }-a}$ (đpcm).

Trong ΔADB, ta có: MN // AB (gt)

Suy ra:  hệ quả định lí ta-lét) (1)

Trong ΔACB, ta có: PQ // AB (gt)

Suy ra: 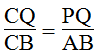 Hệ quá định lí Ta-lét) (2)

Lại có: NQ // AB (gt)

       AB // CD (gt)

Suy ra: NQ // CD

Trong ΔBDC, ta có: NQ // CD (chứng minh trên)

Suy ra: 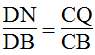(Định lí Ta-lét) (3)

Từ (1), (2) và (3) suy ra 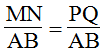 hay MN = PQ.

Lấy D là trung điểm của cạnh BC. 

Khi đó, AD là đường trung tuyến của tam giác ABC.

Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.

Ta có $\frac{AG}{AD}=\frac{2}{3}$ hay $AG=\frac{2}{3}AD$.

Vì MG // AB, theo định lí Thalès, ta suy ra: $\frac{AG}{AD}=\frac{BM}{BD}=\frac{2}{3}$.

Ta có BD = CD (vì D là trung điểm của cạnh BC) nên $\frac{BM}{BC}=\frac{BM}{2BD}=\frac{2}{2.3}=\frac{1}{3}$.

Do đó $BM=\frac{1}{3}BC$ (đpcm).

Ta có:AB//CD(ádhqđl thales)

=>OA/OC=OB/ODhệ quả định lý thales

=>OA.OD=OB.OC   

Ta có ED // AC suy ra 

$\frac{AE}{A}=\frac{CD}{CB}$ (định lí Thales trong tam giác)

          FD // AB suy ra $\frac{AF}{AC}=\frac{BD}{BC}$ (định lí Thales trong tam giác).

Suy ra $\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1.$

Ta có ABCD là hbh 

=>AD=BC,AD//BC

=>góc ADB=góc CBD(slt)

Xét tam giác ADH và CBK có 

AHD=CKB

AD=BC

ADH=CBK

=>Tam giác ADH=CBK(chgn)

=>AH=CK

xét tứ giác AHCK có :

AH//CK(AH vuông DB, CK vuông BD)

AH=CK

=> AHCK là hbh

b) ta có AHCK là hbh 

=>AC cắt HK tại trđ

mà I là trđ HK=>I là trđ AC

do ABCD Là hbh => AC cắt BD tại trđ

mà I là trđ của AC nên I là trđ của BD 

=>BI=ID

a)ta có AD =BC 

mà F là tđ BC E là tđ AD 

=> AE=ED=BF=FC

Xét tứ giác EDFB có 

ED=BF

ED//BF(AD//BC)

=>EDFB là hbh

b)ta có O là tđ của DB 
=>B,O,D Thg hàng

BD cắt EF tại tđ (EBFD là hbh)

Mà O là trđ của BD

=> O là trđ của EF

=> F,O,E thẳng hàng

Ta có :Tt BM cắt tt CN tại G 

=>NG =1/2CG(1)

MG=1/2BG(2)

mà Q là tđ của GC(3)

P là tđ của BG(4)

Từ (1),(3) suy ra NG = GQ

từ (2),(4) suy ra MG=PQ

Xét tứ giác NMQP có

NG=GQ

PG=GM

Mà NQ và PM là 2 đg chéo

=>NMQP là hbh

a)Ta có:AB=BE=1/2AE(B là TĐ của AE)

DC=CF=1/2DF(C là TĐ của DF)

Mà AB=DC(ABCD là hình bình hành)

Suy ra AB=BE=DC=CF

Suy ra AE=DF (1)

Ta có :AB//DC(ABCD là hình bình hành) 

Suy ra AE//DF(2)

Từ(1)và(2)ta đc:AEFD là hình bình hành (dhnb)

Tứ giác ABFC có AB=CF (cmt)

         AB//DC hay AB//CF

suy ra ABFC là hình bình hành 

b)  Ta có :AEFD là hình bình hành 

Suy ra AF cắt ED tại trung điểm của mỗi đường (1)

Ta có ABFC là hình bình hành 

Suy ra AF cắt BC tại TĐ của mỗi đường (2)

Từ (1) và (2) ta đc AF,DE,BC có các TĐ trùng nhau

a)Ta có:AB=BE=1/2AE(B là TĐ của AE)

DC=CF=1/2DF(C là TĐ của DF)

Mà AB=DC(ABCD là hình bình hành)

Suy ra AB=BE=DC=CF

Suy ra AE=DF (1)

Ta có :AB//DC(ABCD là hình bình hành) 

Suy ra AE//DF(2)

Từ(1)và(2)ta đc:AEFD là hình bình hành (dhnb)

Tứ giác ABFC có AB=CF (cmt)

         AB//DC hay AB//CF

suy ra ABFC là hình bình hành 

b)  Ta có :AEFD là hình bình hành 

Suy ra AF cắt ED tại trung điểm của mỗi đường (1)

Ta có ABFC là hình bình hành 

Suy ra AF cắt BC tại TĐ của mỗi đường (2)

Từ (1) và (2) ta đc AF,DE,BC có các TĐ trùng nhau