\(\dfrac{3^6.4^6-12^5}{11.12^5}=\dfrac{\left(3.4\right)^6-12^5}{11.12^5}=\dfrac{12^6-12^5}{11.12^5}=\dfrac{12^5.\left(12-1\right)}{11.12^5}=\dfrac{12^5.11}{11.12^5}=1\)

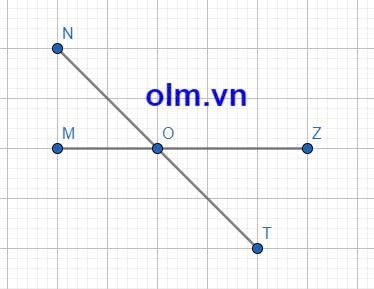
Ta có: \(\widehat{AOD}+\widehat{DOB}=180^0\)(hai góc kề bù)

=>\(5x+4x=180^0\)

=>\(9x=180^0\)

=>\(x=20^0\)

Ta có: \(\widehat{COB}=\widehat{AOD}\)(hai góc đối đỉnh)

mà \(\widehat{AOD}=5x=5\cdot20^0=100^0\)

nên \(\widehat{COB}=100^0\)

Ta có: \(\widehat{AOC}+\widehat{COB}=180^0\)(hai góc kề bù)

=>\(\widehat{AOC}=180^0-100^0=80^0\)

LGBT(Nam+Nữ)

👨‍❤️‍💋‍👨 dụng ko

tao là fan CR7

Tao phan CR7 chứ ko phải Messi

2x=3y nên x/3=y/2 nên x/15=y/10

4y=5z nên y/5=z/4 nên y/10=z/8

Nên x/15=y/10=z/8

Aps dụng tính chất dãy tỉ số bằng nhau ta có:

x/15=y/10=z/8=x+y+x/15+10+8=11/33=1/3

Đến đây dễ rồi nha bạn

\(2x=3y\Rightarrow\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{3\times5}=\frac{y}{2\times5}\Rightarrow\frac{x}{15}=\frac{y}{10}\) (1)

\(4y=5z\Rightarrow\frac{y}{5}=\frac{z}{4}\Rightarrow\frac{y}{5\times2}=\frac{z}{4\times2}\Rightarrow\frac{y}{10}=\frac{z}{8}\) (2)

Từ (1) và (2):

\(\frac{x}{15}=\frac{y}{10}=\frac{z}{8}=\frac{x+y+z}{15+10+8}=\frac{11}{33}=\frac{1}{3}\)

• \(\frac{x}{15}=\frac{1}{3}\Rightarrow x=\frac{1}{3}\times15=5\)
• \(\frac{y}{10}=\frac{1}{3}\Rightarrow y=\frac{1}{3}\times10=\frac{10}{3}\)
• \(\frac{z}{8}=\frac{1}{3}\Rightarrow z=\frac{1}{3}\times8=\frac{8}{3}\)

Đặt \(2x^2+3x+5=0\)

=>\(2\left(x^2+\dfrac{3}{2}x+\dfrac{5}{2}\right)=0\)

=>\(x^2+\dfrac{3}{2}x+\dfrac{5}{2}=0\)

=>\(x^2+2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}+\dfrac{31}{16}=0\)

=>\(\left(x+\dfrac{3}{4}\right)^2+\dfrac{31}{16}=0\)(vô lý)

=>Đa thức \(2x^2+3x+5\) không có nghiệm

         Giải:

Ta có: A = 2\(x^2\) + 3\(x\) + 5 

A = 2(\(x^2\) + \(x.\dfrac{3}{4}\)) + (\(\dfrac{3}{4}\)\(x\) + \(\dfrac{9}{4}\)) + 5

A = 2.\(x\)(\(x+\dfrac{3}{4}\)) + \(\dfrac{3}{2}\).(\(x+\dfrac{3}{4}\)) + \(\dfrac{31}{8}\) 

A = 2(\(x+\dfrac{3}{4}\))(\(x\) + \(\dfrac{3}{4}\)) + \(\dfrac{31}{8}\)

A = 2.(\(x+\dfrac{3}{4}\))² + \(\dfrac{31}{8}\)

Vì (\(x+\dfrac{3}{4}\))² ≥ 0; ⇒ 2.(\(x+\dfrac{3}{4}\))² ≥ 0 

⇒ A ≥ \(\dfrac{31}{8}\) > 0

Vậy phương trình đã cho vô nghiệm (đpcm)

cứu mik

A = (\(\dfrac{-7}{2}\))²²²² \(\times\) (- \(\dfrac{2}{999}\))¹²³⁴

A = \(\dfrac{7^{2222}}{2^{2222}}\) \(\times\) \(\dfrac{2^{1234}}{9^{1234}}\)

A = \(\dfrac{7^{2222}}{9^{1234}}\) \(\times\) \(\dfrac{2^{1234}}{2^{2222}}\)

A = \(\dfrac{7^{2222}}{9^{1234}}\) \(\times\) \(\dfrac{1}{2^{988}}\)

A = \(\dfrac{7^{2222}}{9^{1234}\times2^{988}}\)

cảm ơn cô 

`3^39 < 3^40 = 9^20 < 11^21`

3³⁹ < 3⁴⁰ = (3²)²⁰ = 9²⁰ < 11²⁰ < 11²¹

Vậy 3³⁹ < 11²¹