Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

=>\(\widehat{B}+70^0+40^0=180^0\)

=>\(\widehat{B}=70^0\)

Ta có: \(\widehat{xAB}+\widehat{ABC}=70^0+110^0=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên Ax//BC

20

`12 - 5 + 13`

`= 7 + 13`

`= 20`

    22 - 12 + 56 - 31 + 67 + 12 - 22

= (56 - 31 + 67) + (22 - 22) - (12 - 12)

= (25 + 67) + 0 + 0

=     92      

Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB~ΔOCD

=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)(1)

Xét ΔOBP và ΔODQ có

\(\widehat{OBP}=\widehat{ODQ}\)(BP//DQ)

\(\widehat{BOP}=\widehat{DOQ}\)(hai góc đối đỉnh)

Do đó: ΔOBP~ΔODQ

=>\(\dfrac{OB}{OD}=\dfrac{OP}{OQ}\left(2\right)\)

Xét ΔOAM và ΔOCN có

\(\widehat{OAM}=\widehat{OCN}\)(AM//CN)

\(\widehat{AOM}=\widehat{CON}\)(hai góc đối đỉnh)

Do đó: ΔOAM~ΔOCN

=>\(\dfrac{OA}{OC}=\dfrac{OM}{ON}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\dfrac{OP}{OQ}=\dfrac{OM}{ON}\)

=>\(OP\cdot ON=OM\cdot OQ\)

Bài 1:

Gọi số lập được có dạng là \(\overline{abc}\)

c có 3 cách chọn

a có 6 cách chọn

b có 5 cách chọn

Do đó: Có \(3\cdot6\cdot5=90\left(số\right)\) lập được

Số số tự nhiên có 3 chữ số phân biệt lập được là \(7\cdot6\cdot5=210\left(số\right)\)

Xác suất để số được chọn là số chẵn là \(\dfrac{90}{210}=\dfrac{3}{7}\)

Bài 2:

Số cách chọn ngẫu nhiên 4 quả cầu là: \(C^4_{10}\)

Số cách chọn 4 quả cầu trắng là: \(C^4_4\)(cách)

Số cách chọn 4 quả cầu xanh là \(C^4_6\left(cách\right)\)

Xác suất để chọn được 4 quả cầu cùng màu là:

\(\dfrac{C_4^4+C_6^4}{C_{10}^4}=\dfrac{8}{105}\)

Đặt: \(n^2+3n+90=k^2\)

\(=>4n^2+12n+360=4k^2\\ =>\left(4n^2+12n+9\right)+351=4k^2\\ =>\left(2n+3\right)^2-4k^2=-351\\ =>\left(2n-2k+3\right)\left(2n+2k+3\right)=-351\)

Vì n là số tự nhiên nên: \(=>2n+2k+3>2n-2k+3\)

Ta có các trường hợp sau: 

TH1: \(\left\{{}\begin{matrix}2n+2k+3=27\\2n-2k+3=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=2\\k=10\end{matrix}\right.\left(tm\right)\)

TH2: \(\left\{{}\begin{matrix}2n+2k+3=13\\2n-2k+3=-27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-5\\k=10\end{matrix}\right.\left(ktm\right)\)

TH3: \(\left\{{}\begin{matrix}2n+2k+3=9\\2n-2k+3=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-9\\k=12\end{matrix}\right.\left(ktm\right)\)

TH4: \(\left\{{}\begin{matrix}2n+2k+3=39\\2n-2n+3=-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=6\\k=12\end{matrix}\right.\left(tm\right)\) 

TH5: \(\left\{{}\begin{matrix}2n+2k+3=3\\2n-2k+3=-117\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-30\\k=30\end{matrix}\right.\left(ktm\right)\)

TH6: \(\left\{{}\begin{matrix}2n+2k+3=117\\2n-2k+3=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{57}{2}\\k=\dfrac{57}{2}\end{matrix}\right.\) (ktm) 

TH7: \(\left\{{}\begin{matrix}2n+2k+3=351\\2n-2k+3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{175}{2}\\k=88\end{matrix}\right.\left(ktm\right)\)

TH8: \(\left\{{}\begin{matrix}2n+2k+3=1\\2n-2k+3=-351\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=-89\\k=88\end{matrix}\right.\)

Vậy n = 2 hoặc n = 6 

Các số chia hết cho 13 trong khoảng từ 1 đến 100 là: 13;26;39;52;65;78;91

=>Có 7 số

có 7 số: 13, 26, 39, 52, 65, 78, 91

Bài 1:

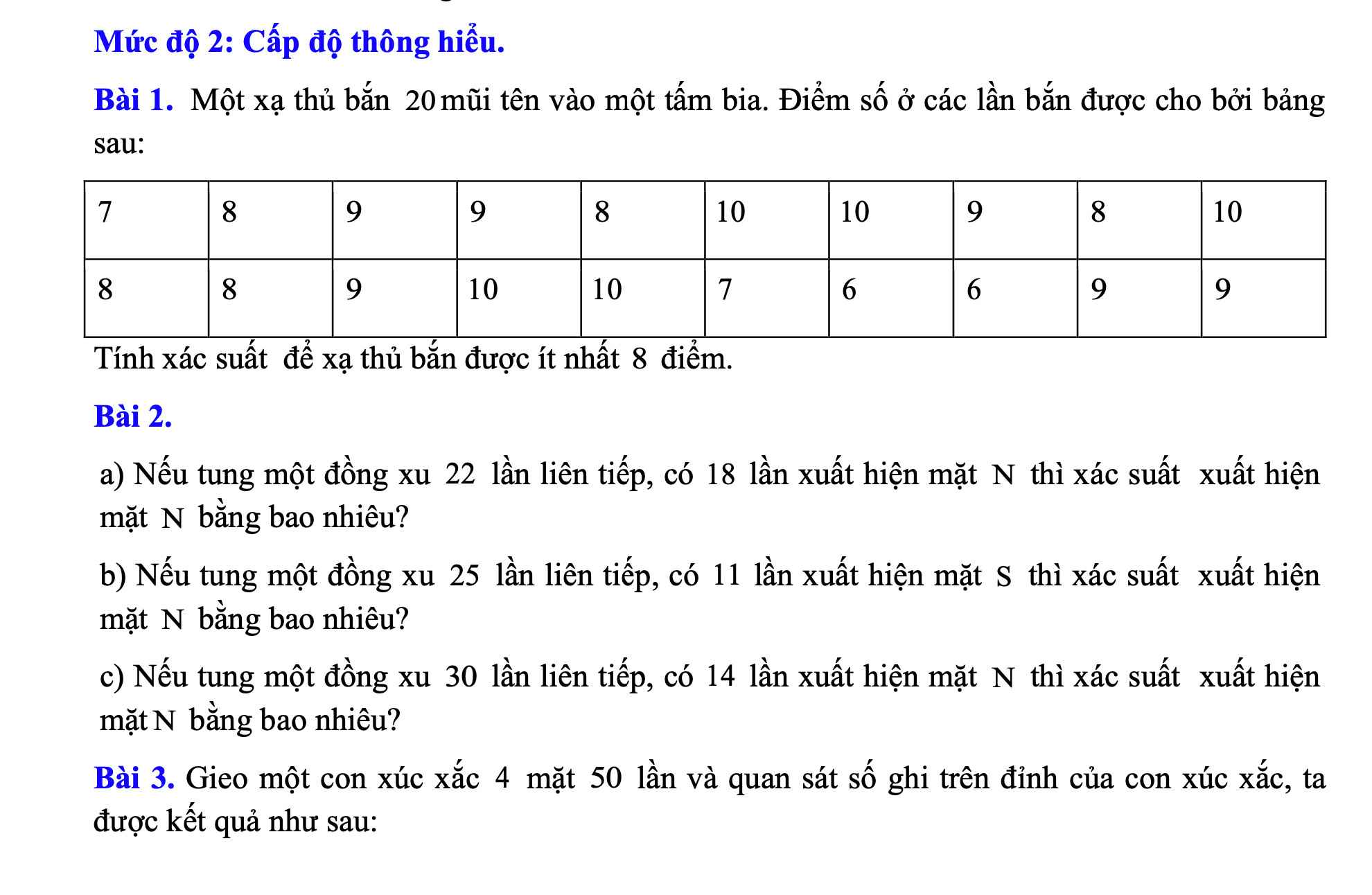
Số lần bắn được ít nhất 8 điểm là:

5+6+5=16(lần)

=>Xác suất để bắn được ít nhất 8 điểm là \(P=\dfrac{16}{20}=\dfrac{4}{5}\)

Bài 2:

a: Xác suất xuất hiện mặt N là: \(\dfrac{18}{22}=\dfrac{9}{11}\)

b: Số lần xuất hiện mặt S là 25-11=14(lần)

Xác suất xuất hiện mặt S là \(\dfrac{14}{25}\)

c: Xác suất xuất hiện mặt N là \(\dfrac{14}{30}=\dfrac{7}{15}\)

\(\left(x+\sqrt{3+x^2}\right)\left(y+\sqrt{3+y^2}\right)=3\\ < =>\left(x+\sqrt{3+x^2}\right)\left(x-\sqrt{3+x^2}\right)\left(y+\sqrt{3+y^2}\right)=3\left(x-\sqrt{3+x^2}\right)\\ < =>x^2-3-x^2\left(y+\sqrt{3+y^2}\right)=3\left(x-\sqrt{3+x^2}\right)\\ < =>-\left(y+\sqrt{3+y^2}\right)=x-\sqrt{3+x^2}\left(1\right)\)

Tương tự ta có: \(x+\sqrt{3+x^2}=-\left(y-\sqrt{3+y^2}\right)\left(2\right)\)

Lấy (1) + (2) ta có: 

\(-\left(y+\sqrt{3+y^2}\right)-\left(y-\sqrt{3+y^2}\right)=x-\sqrt{3+x^2}+x+\sqrt{3+x^2}\\ < =>-2y=2x\\ < =>2x+2y=0\\ < =>x+y=0\)